Comônadas
Esse post é baseado no livro Teoria das Categorias para Programadores, de Bartosz Milewski.
1 Comonads
A categoria oposta da Kleisli, denominada co-Kleisli leva ao conceito
de Comonads. Agora temos endofunctors w (m de cabeça para baixo) e
morfismos do tipo w a -> b, e queremos definir um operador de
composição para eles, da mesma forma que definimos o operador >=>:
(=>=) :: (w a -> b) -> (w b -> c) -> (w a -> c)
Da mesma forma, nosso morfismo identidade é similar ao return mas com
a seta invertida:
extract :: w a -> a
Chamamos essa função de extract pois ela permite extrair um conteúdo
do functor w (nosso container).
O oposto de nosso operador bind deve ter a assinatura
(w a -> b) -> w a -> w b, ou seja, dada uma função que retira um valor
do tipo a de um container transformando em um tipo b no processo,
retorne uma função que, dado um w a me retorne um w b. Essa função é
chamada de extend ou na forma de operador =>>.
Finalmente, o oposto de join é o duplicate, ou seja, insere um
container dentro de outro container, sua assinatura é w a -> w (w a).
Nesse ponto, podemos perceber a dualidade entre Monad e Comonad. Em um
Monad criamos uma forma de colocar um valor dentro de um container,
através do return, mas sem garantias de que poderemos retirá-lo de lá.
Envolvemos nosso valor em um contexto computacional, que pode ficar
escondido até o final do programa, como vimos no comportamento do Monad
IO.
Já um Comonad, nos traz uma forma de retirar um valor de um container,
através de extract, sem prover uma forma de colocá-lo de volta. Além
disso, ele permite uma computação contextual de um elemento do
container, ou seja, podemos focar em um elemento e manter todo o
contexto em volta dele (e já vimos isso nos tipos buracos!).
Então nossa classe Comonad é definida por:
class Functor w => Comonad w where
(=>=) :: (w a -> b) -> (w b -> c) -> (w a -> c)
extract :: w a -> a
(=>>) :: (w a -> b) -> w a -> w b
duplicate :: w a -> w (w a)
2 Reader Comonad
Relembrando o Reader Monad que definimos no post anterior:
data Reader e a = Reader (e -> a)
instance Monad (Reader e) where
-- (Reader e a) -> (a -> Reader e b) -> (Reader e b)
-- (Reader f) >>= k = \e -> runReader (k (f e)) e
ra >>= k = Reader (\e -> let a = runReader ra e
rb = k a
in runReader rb e)
return a = Reader (\e -> a)
A versão embelezada dos morfismos na categoria Kleisli é
a -> Reader e b que pode ser traduzido para a -> (e -> b) e colocado
na forma curry de (a, e) -> b. Com isso, conseguimos definir o
Comonad de Writer e como o complemento do Monad Reader:
instance Comonad (Writer e) where
(=>=) :: (Writer e a -> b) -> (Writer e b -> c) -> (Writer e a -> c)
f =>= g = \(Writer e a) -> let b = f (Writer e a)
c = g (Writer e b)
in c
extract (Writer e a) = a
Basicamente, a função extract ignora o ambiente definido por e e
retorna o valor a contido no container. O operador de composição
simplesmente pega duas funções que recebem tuplas como parâmetros, sendo
a primeira do mesmo tipo, e aplica sequencialmente utilizando o mesmo
valor de e nas duas chamadas (afinal e é read-only).
3 Definições padrão
Examinando o operador =>= temos como argumentos f :: w a -> b e
g :: w b -> c e precisamos gerar uma função h :: w a -> c. Para
gerar um valor do tipo c, dado f, g, a única possibilidade é aplicar
g em um tipo w b:
f =>= g = g ...
Tudo que temos a disposição é uma função f que produz um b.
Precisamos então de uma função com a assinatura
(w a -> b) -> w a -> w b, que é nossa função extend (=>>). Com
isso temos a definição padrão:
f =>= g = \wa -> g . (f ==>) wa
-- ou
-- f =>= g = g . (f =>>)
Da mesma forma, pensando no operador =>> com assinatura
(w a -> b) -> w a -> w b, percebemos que não tem como obter
diretamente um w b ao aplicar a função argumento em w a. Porém, uma
vez que w necessariamente é um Functor, temos a disposição a função
fmap :: (c -> b) -> w c -> w b, que ao fazer com que c = w a, temos
(w a -> b) -> w (w a) -> w b. Se conseguirmos produzir um w (w a),
podemos utilizar fmap para implementar =>>. Temos a função
duplicate, o que faz com que:
class Functor w => Comonad w where
extract :: w a -> a
(=>=) :: (w a -> b) -> (w b -> c) -> (w a -> c)
f =>= g = g . (=>>)
(=>>) :: (w a -> b) -> w a -> w b
f =>> wa = fmap f . duplicate
duplicate :: w a -> w (w a)
duplicate = (id =>>)
A ideia de um Comonad é que você possui um container com um ou mais
valores de a e que existe uma noção de valor atual ou foco em um
dos elementos. Esse valor atual é acessado pela função extract. O
operador co-peixe (=>=) faz alguma computação, definida pelas
funções compostas, no valor atual porém tendo acesso a tudo que está em
volta dele. Já a função duplicate cria diversas versões de w a cada
qual com um foco diferente, ou seja, temos todas as possibilidades de
foco para aquela estrutura. Finalmente, a função extend (=>>),
primeiro gera todas as versões da estrutura via duplicate para então
aplicar a função co-Kleisli através do fmap, ou seja, ela aplica a
função em todas as possibilidades de foco.
4 Stream de Dados
Podemos definir um Stream de dados como uma lista infinita não-vazia:
data Stream a = Cons a (Stream a)
instance Functor Stream where
fmap f (Cons a as) = Cons (f a) (fmap f as)
Notem que essa estrutura possui naturalmente um foco em seu primeiro
elemento. Com isso podemos definir a função extract simplesmente como:
extract (Cons a _) = a
Lembrando que a função duplicate deve gerar uma Stream de Streams,
cada uma focando em um elemento dela, podemos criar uma definição
recursiva como:
duplicate (Cons a as) = Cons (Cons a as) (duplicate as)
Cada chamada recursiva cria uma Stream com a cauda da lista original. Com isso temos as funções necessárias para criar uma instância de Comonad para Streams:
instance Comonad Stream where
extract (Cons a _) = a
duplicate (Cons a as) = Cons (Cons a as) (duplicate as)
Como exemplo de aplicação vamos criar uma função que calcula a média móvel de um stream de dados. Começamos com a definição da média entre os \(n\) próximos elementos:
sumN :: Num a => Int -> Stream a -> a
sumN n (Cons a as) | n <= 0 = 0
| otherwise = a + sumN (n-1) as
avgN :: Fractional a => Int -> Stream a -> a
avgN n as = (sumN n as) / (fromIntegral n)
Notem que avgN tem assinatura Int -> (w a -> a), para gerarmos uma
Stream de médias móveis queremos algo como
Int -> (w a -> a) -> w a -> w a, que remete a assinatura de =>>:
movAvg :: Fractional a => Int -> Stream a -> Stream a
movAvg n as = (avgN n) =>> as
Com isso, a função avgN n será aplicada em cada foco de as gerando
uma nova Stream contendo apenas os valores das médias.
Podemos implementar o Comonad Stream em Python criando uma lista ligada em que o próximo elemento é definido por uma função geradora passada como parâmetro para o construtor de objetos da classe:
from functools import partial
class Stream:
'''
Data Stream in Python: infinite stream of data with generator function
-- equivalent to Haskell Stream a = Stream a (Stream a)
x: initial value
f: generator function (id if None)
g: mapped function (Fucntor fmap)
'''
def __init__(self, x=1, f=None, g=None):
idfun = lambda x: x
self.f = idfun if f is None else f
self.g = idfun if g is None else g
self.x = x
def __str__(self):
x = self.extract()
return f"{x}..."
def next(self):
''' the tail of the Stream '''
return Stream(self.f(self.x), self.f, self.g)
def extract(self):
''' returns mapped current value '''
return self.g(self.x)
def duplicate(self):
''' a Stream of Streams '''
def nextS(xs):
return self.next()
return Stream(self, nextS)
def fmap(self, g):
''' Functor instance '''
return Stream(self.x, self.f, g)
def extend(self, g):
''' comonad extend =>> '''
return self.duplicate().fmap(g)
def avgN(n, xs):
s = 0
for i in range(n):
s += xs.extract()
xs = xs.next()
return s/n
def movAvg(n, xs):
movAvgN = partial(avgN, n)
return xs.extend(movAvgN)
def f(x):
return x+1
xs = Stream(1, f)
print(xs)
print(movAvg(5, xs))
5 Store Comonad
Relembrando o State Monad visto anteriormente, ele foi definido como a
composição (Reader s) . (Writer s):
data State s a = State (s -> (a, s))
= Reader s (Writer s a)
Isso foi possível pois os Functors Reader e Writer são adjuntos. De
forma análoga podemos fazer a composição complementar para criarmos um
Comonad:
data Store s a = Store (s -> a) s
= Writer s (Reader s a)
A instância de Functor para esse Comonad é simplesmente a composição da
função definida por Reader s a:
instance Functor (Store s) where
fmap g (Store f s) = Store (g . f) s
A assinatura de extract deve ser Store s a -> a, sendo que o tipo
Store armazena uma função s -> a e um s, basta aplicar a função no
estado s que ele armazena. Por outro lado, a função duplicate pode
se aproveitar da aplicação parcial na construção de um valor definindo:
instance Comonad (Store s) where
extract (Store f s) = f s
duplicate (Store f s) = Store (Store f) s
Podemos imaginar o Comonad Store como um par que contém um container
(a função f) que armazena diversos elementos do tipo a indexados
pelo tipo s (i.e., array associativa) e um s que indica o foco
atual da estrutura (como em um Zipper, visto anteriormente). Nessa
interpretação temos que extract retorna o elemento a na posição
atual s e duplicate simplesmente cria infinitas cópias desse
container de tal forma que cada cópia está deslocada em \(n\) posições
para direita ou para a esquerda.
Como exemplo, vamos implementar o automato celular 1D conforme descrito por Wolfram. Esse automato inicia com uma lista infinita indexada por valores inteiros (positivos e negativos) e centralizada em \(0\). A lista contém inicialmente o valor \(1\) na posição central e \(0\) em todas as outras posições.
A cada passo da iteração, a lista é atualizada através das regras n em
que \(0 \leq n \leq 255\). A numeração da regra codificam um mapa de
substituição para o número binário formado pela subslita composta do
valor atual e de seus dois vizinhos. Por exemplo, a regra 30 codifica:
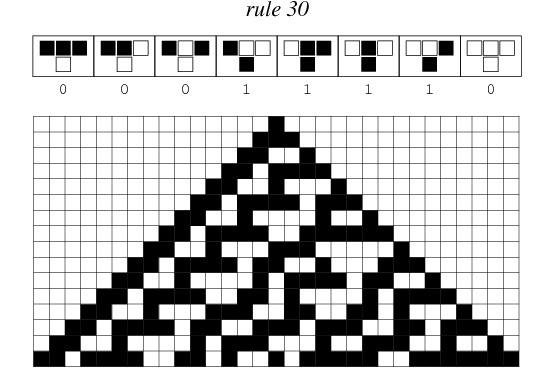
Figure 1: FONTE: http://mathworld.wolfram.com/Rule30.html
Podemos implementar esse autômato utilizando um Store Int Int,
primeiro definindo a função que aplica a regra:
rule :: Int -> Store Int Int -> Int
rule x (Store f s) = (succDiv2 !! bit) `rem` 2
where
-- qual o bit que devemos recuperar
bit = (f (s+1)) + 2*(f s) + 4*(f (s-1))
-- divisao sucessiva de x por 2
succDiv2 = iterate (`div` 2) x
Fazendo uma aplicação parcial do número da regra, a assinatura da função
fica: Store Int Int -> Int que deve ser aplicada em um Store Int Int
para gerar a próxima função de indexação. Isso sugere o uso de extend
(=>>):
nextStep rl st = rl =>> st
Mas queremos uma aplica sucessiva dessa regra infinitamente, para isso
podemos utilizar iterate:
wolfram :: (Store Int Int -> Int) -> Store Int Int -> [Store Int Int]
wolfram rl st = iterate (rl =>> st)
A representação inicial de nosso ambiente é feita por:
f0 :: Int -> Int
f0 0 = 1
f0 _ = 0
fs :: Store Int Int
fs = Store f0 0
Finalmente, podemos capturar um certo instante do nosso autômato simplesmente acessando o elemento correspondente da lista:
wolf30 = wolfram (rule 30) fs
fifthIteration = wolf30 !! 5
E podemos imprimir nosso ambiente criando uma instância de Show:
instance (Num s, Enum s, Show a) => Show (Store s a) where
show (Store f s) = show [f (s+i) | i <- [-10 .. 10]]
main = print (take 5 wolf30)
Como referência, o código em Python ficaria:
from functools import partial
import itertools
class Store:
def __init__(self, f, s):
self.f = f
self.s = s
def fmap(self, g):
f = lambda s: g(self.f(s))
return Store(f, self.s)
def extract(self):
return self.f(self.s)
def duplicate(self):
return Store(lambda s: Store(self.f, s), self.s)
def extend(self, g):
return self.duplicate().fmap(g)
def __str__(self):
return str([self.f(self.s+i) for i in range(-10,11)])
def rule(x, fs):
succDiv2 = [x]
while x!=0:
x = x//2
succDiv2.append(x)
bit = fs.f(fs.s+1) + 2*fs.f(fs.s) + 4*fs.f(fs.s-1)
if bit >= len(succDiv2):
return 0
return succDiv2[bit] % 2
def wolfram(rl, fs):
while True:
yield fs
fs = fs.extend(rl)
def f0(x):
if x==0:
return 1
return 0
fs = Store(f0, 0)
wolf30 = wolfram(partial(rule, 30), fs)
top5 = itertools.islice(wolf30, 6)
for w in top5:
print(w)
6 Referências
https://bartoszmilewski.com/2014/10/28/category-theory-for-programmers-the-preface/