Grupo de Estudos em Haskell da UFABC > Introdução à Programação Funcional em Haskell > Conceitos Básicos - Parte 2

Conceitos Básicos - Parte 2

Playlists

1 Polimorfismo

Considere a função length que retorna o tamanho de uma lista. Ela deve funcionar para qualquer uma dessas listas:

[1,2,3,4] :: [Int]
[False, True, True] :: [Bool]
['o', 'l', 'a'] :: [Char]

Pergunta

Qual é, então, o tipo de length?

length :: [a] -> Int

Quem é a?

Em Haskell, a é conhecida como variável de tipo e ela indica que a função deve funcionar para listas de qualquer tipo.
As variáveis de tipo devem seguir a mesma convenção de nomes do Haskell, iniciar com letra minúscula.
Como convenção utilizamos a, b, c,....

1.1 Overloaded types

Considere agora a função (+), diferente de length ela pode ter um comportamento diferente para tipos diferentes.
Internamente somar dois Int pode ser diferente de somar dois Integer (e definitivamente é diferente de somar dois Float).
Ainda assim, essa função deve ser aplicada a tipos numéricos.

A ideia de que uma função pode ser aplicada a apenas uma classe de tipos é explicitada pela Restrição de classe (_ class constraint _).
Uma restrição é escrita na forma C a, onde C é o nome da classe e a uma variável de tipo.

(+) :: Num a => a -> a -> a

A função (+) recebe dois tipos de uma classe numérica e retorna um valor desse mesmo tipo.

Note que nesse caso, ao especificar a entrada como Int para o primeiro argumento, todos os outros devem ser Int também.

(+) :: Num a => a -> a -> a

Uma vez que uma função contém uma restrição de classe, pode ser necessário definir instâncias dessa função para diferentes tipos pertencentes à classe.
Os valores também podem ter restrição de classe:

3 :: Num a => a

O que resolve nosso problema anterior.

Tire da cabeça os conceitos de Classe e Instância vindos de orientação a objetos. Aqui uma classe de tipos nada mais é que um conjunto, uma coleção, uma lista de tipos. Por sua vez, uma instância nada mais é que dizer que um tipo pertence a uma classe, ou seja, está dentro daquele conjunto de classes. Mais sobre isso aqui.

1.2 Exemplos de funções

impar :: Integral a => a -> Bool
impar n = n `mod` 2 == 1

quadrado :: Num a => a -> a
quadrado n = n*n

quadradoMais6Mod9 :: Integral a => a -> a
quadradoMais6Mod9 n = (n*n + 6) `mod` 9

1.3 Exercício 1

Escreva uma função que retorne a raíz de uma equação do segundo grau:

raiz2Grau :: Floating a => a -> a -> a -> (a, a)
raiz2Grau a b c = ( ???, ??? )

Teste com raiz2Grau 4 3 (-5) e raiz2Grau 4 3 5.

1.4 Resposta 1

raiz2Grau :: Floating a => a -> a -> a -> (a, a)
raiz2Grau a b c = ( ((-b) + sqrt (b^2 - 4*a*c)) / (2*a),
		    ((-b) - sqrt (b^2 - 4*a*c)) / (2*a) )

raiz2Grau 4 3 (-5)
raiz2Grau 4 3 5

Saída:


(0.8042476415070754,-1.5542476415070754)
(NaN,NaN)

1.5 Cláusula where

Para organizar nosso código, podemos utilizar a cláusula where para definir nomes intermediários:

f x = y + z
  where
    y = e1
    z = e2

Exemplo:

euclidiana :: Floating a => (a, a) -> (a, a) -> a
euclidiana (px, py) (qx, qy) = sqrt diffSq
  where
    diffSq = ((px - qx)^2) + ((py - qy)^2)

1.6 Exercício 2

Reescreva a função raiz2Grau utilizando where.

1.7 Resposta 2

Escreva uma função que retorne a raíz de uma equação do segundo grau:

raiz2Grau :: Floating a => a -> a -> a -> (a, a)
raiz2Grau a b c = (x1, x2)
  where
    x1      = ((-b) + sqDelta) / (2*a)
    x2      = ((-b) - sqDelta) / (2*a)
    sqDelta = sqrt delta
    delta   = b^2 - 4*a*c

1.8 Condicionais

A função if-then-else nos permite utilizar desvios condicionais em nossas funções:

abs :: Num a => a -> a
abs n = if (n >= 0) then n else (-n)

abs :: Num a => a -> a
abs n = if (n >= 0)
	then n
	else (-n)

Também podemos encadear condicionais:

signum :: (Ord a, Num a) => a -> a
signum n = if (n == 0)
	   then 0
	   else if (n > 0)
		then 1
		else (-1)

1.9 Exercício 3

Utilizando condicionais, reescreva a função raiz2Grau para retornar (0,0) no caso de delta negativo.
Note que a assinatura da função agora deve ser:

raiz2Grau :: (Ord a, Floating a) => a -> a -> a -> (a, a)

1.10 Resposta 3

raiz2Grau :: (Ord a, Floating a) => a -> a -> a -> (a, a)
raiz2Grau a b c = (x1, x2)
  where
    x1 = if delta >= 0
	 then ((-b) + sqDelta) / (2*a)
	 else 0
    x2 = if delta >= 0
	 then ((-b) - sqDelta) / (2*a)
	 else 0
    sqDelta = sqrt delta
    delta = b^2 - 4*a*c

raiz2Grau 4 3 (-5)
raiz2Grau 4 3 5

Saída:


(0.8042476415070754,-1.5542476415070754)
(0.0,0.0)

1.11 Expressões guardadas (Guard Expressions)

Uma alternativa ao uso de if-then-else é o uso de guards (|) que deve ser lido como tal que:

signum :: (Ord a, Num a) => a -> a
signum n | n == 0    =  0  -- signum n tal que n==0
			   -- é definido como 0
	 | n > 0     =  1
	 | otherwise = -1

otherwise é o caso contrário e é definido como otherwise = True.

Note que as expressões guardadas são avaliadas de cima para baixo, o primeiro verdadeiro será executado e o restante ignorado.

classificaIMC :: Double -> String
classificaIMC imc
    | imc <= 18.5 = "abaixo do peso"
    -- não preciso fazer && imc > 18.5
    | imc <= 25.0 = "no peso correto"
    | imc <= 30.0 = "acima do peso"
    | otherwise   = "muito acima do peso"

1.12 Exercício 4

Utilizando guards, reescreva a função raiz2Grau para retornar um erro com delta negativo.
Para isso utilize a função error:

error "Delta negativo."

1.13 Resposta 4

raiz2Grau :: (Ord a, Floating a) => a -> a -> a -> (a, a)
raiz2Grau a b c
  | delta >= 0   = (x1, x2)
  | otherwise    = error "Delta negativo."
  where
    x1      = ((-b) + sqDelta) / (2*a)
    x2      = ((-b) - sqDelta) / (2*a)
    sqDelta = sqrt delta
    delta   = b^2 - 4*a*c

raiz2Grau 4 3 (-5)
raiz2Grau 4 3 5

Saída:


(0.8042476415070754,-1.5542476415070754)
*** Exception: Delta negativo.
CallStack (from HasCallStack):
  error, called at :175:20 in interactive:Ghci103

O uso de error interrompe a execução do programa. Nem sempre é a melhor forma de tratar erro, aprenderemos alternativas ao longo do curso.

1.14 Pattern Matching

Considere a seguinte função:

not :: Bool -> Bool
not x = if (x == True) then False else True

Podemos rescrevê-la utilizando guardas:

not :: Bool -> Bool
not x | x == True  = False
      | x == False = True

Quando temos comparações de igualdade nos guardas, podemos definir as expressões substituindo diretamente os argumentos:

not :: Bool -> Bool
not True  = False
not False = True

Não precisamos enumerar todos os casos, podemos definir apenas casos especiais:

soma :: (Eq a, Num a) => a -> a -> a
soma x 0 = x
soma 0 y = y
soma x y = x + y

Assim como os guards, os padrões são avaliados do primeiro definido até o último.

Trate os casos especiais da multiplicação utilizando Pattern Matching:

mul :: Num a => a-> a -> a
mul x y = x*y

mul :: (Eq a, Num a) => a-> a -> a
mul 0 y = 0
mul x 0 = 0
mul x 1 = x
mul 1 y = y
mul x y = x*y

Quando a saída não depende da entrada, podemos substituir a entrada por _ (não importa):

mul :: (Eq a, Num a) => a-> a -> a
mul 0 _ = 0
mul _ 0 = 0
mul x 1 = x
mul 1 y = y
mul x y = x*y

Como o Haskell é preguiçoso, ao identificar um padrão contendo 0 ele não avaliará o outro argumento.

1.15 Expressões \(\lambda\)

As expressões lambdas , também chamadas de funções anônimas , definem uma função sem nome para uso geral:

-- Recebe um valor numérico e
-- retorna uma função que
-- recebe um número e retorna outro número
somaMultX :: Num a => a -> (a -> a)
somaMultX x = \y -> x + x * y

-- somaMult2 é uma função que
-- retorna um valor multiplicado por 2
somaMult2 = somaMultX 2

1.16 Operadores

Para definir um operador em Haskell, podemos criar na forma infixa ou na forma de função:

(:+) :: Num a => a -> a -> a
x :+ y = abs x + y

(:+) :: Num a => a -> a -> a
(:+) x y = abs x + y

Da mesma forma, uma função pode ser utilizada como operador se envolta de acentos graves:

mod 10 3
10 `mod` 3

Saída:

1
1

Sendo # um operador, temos que (#), (x #), (# y) são chamados de seções , e definem:

(#)   = \x -> (\y -> x # y)
(x #) = \y -> x # y
(# y) = \x -> x # y

Essas formas são também conhecidas como point-free notation :

(/) 4 2
(/2) 4
(4/) 2

Saída:


2.0
2.0
2.0

1.17 Exercício 5

Considere o operador (&&&), simplique a definição para apenas dois padrões:

(&&&) :: Bool -> Bool -> Bool
True  &&& True  = True
True  &&& False = False
False &&& True  = False
False &&& False = False

1.18 Resposta 5

Considere o operador (&&&), simplique a definição para apenas dois padrões:

(&&&) :: Bool -> Bool -> Bool
True &&& True = True
_    &&& _    = False

1.19 Para saber mais

Tipos polimórficos
- [GH] 3; [SGS] 2; [ML] 3
Funções, casamento de padrões, guardas, lambdas
- [GH] 4; [SGS] 2; [ML] 4

2 Listas

Uma das principais estruturas em linguagens funcionais.
Representa uma coleção de valores de um determinado tipo.
Todos os valores devem ser do mesmo tipo.

Definição recursiva: ou é uma lista vazia ou um elemento do tipo genérico a concatenado com uma lista de a.

data [] a = [] | a : [a]

(:) - operador de concatenação de elemento com lista
- Lê-se: _ cons _

Seguindo a definição anterior, a lista [1, 2, 3, 4] é representada por:

lista = 1 : 2 : 3 : 4 :[]

É uma lista ligada!!

lista = 1 : 2 : 3 : 4 :[]

A complexidade das operações são as mesmas da estrutura de lista ligada!

2.1 Criando listas

Existem diversos syntax sugar para criação de listas (ainda bem! 😌)

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

Faixa de valores inclusivos:

[1..10]   == [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

Faixa de valores inclusivos com tamanho do passo:

[0,2..10] == [0, 2, 4, 6, 8, 10]

Lista infinita:

[0,2..]   == [0, 2, 4, 6, 8, 10,..]

Ao infinito e além

Como o Haskell permite a criação de listas infinitas?

Uma vez que a avaliação é preguiçosa, ao fazer:

lista = [0,2..]

ele cria apenas uma promessa de lista.

Efetivamente ele faz:

lista = 0 : 2 : geraProximo

sendo geraProximo uma função que gera o próximo elemento da lista.

Conforme for necessário, ele gera e avalia os elementos da lista sequencialmente.
Então a lista infinita não existe em memória, apenas uma função que gera quantos elementos você precisar dela.

2.2 Para saber mais

Listas
Livros [GH] 5; [SGS] 2; [ML] 2

3 Funções básicas para manipulação de listas

3.1 Recuperar elementos - `!!`

O operador !! recupera o \(i\text{-ésimo}\) elemento da lista, com índice começando do 0:

lista = [0..10]
lista !! 2

Saída:

Note que esse operador é custoso para listas ligadas! Não abuse dele!

3.2 Recuperar elementos - `head`

A função head retorna o primeiro elemento da lista:

head [0..10]

Saída:

Note que esta operação é barata, com custo constante.

3.3 Recuperar elementos - `tail`

A função tail retorna a lista sem o primeiro elemento (sua cauda):

tail [0..10]

Saída:


[1,2,3,4,5,6,7,8,9,10]

Esta operação executa em tempo constante.

3.4 Exercício 6

O que a seguinte expressão retornará?

head (tail [0..10])

3.5 Exercício 6 - Solução

head (tail [0..10])

Saída:

3.6 Recuperar elementos - `take`

A função take retorna os n primeiros elementos da lista:

take 3 [0..10]

Saída:


[0,1,2]

Considerando que a representação interna de listas no Haskell é através de uma lista ligada, qual é a complexidade de take?

3.7 Recuperar elementos - `drop`

E a função drop retorna a lista sem os n primeiros elementos:

drop 6 [0..10]

Saída:


[6,7,8,9,10]

3.8 Exercício 7

Implemente o operador !! utilizando as funções anteriores.

3.9 Exercício 7 - Solução

Implemente o operador !! utilizando as funções anteriores.

xs !! n = head (drop n xs)

3.10 Tamanho da lista - `length`

O tamanho da lista é dado pela função length:

length [1..10]

Saída:

Atenção, a função length é \(O(n)\).

3.11 Somatória e Produtória

As funções sum e product retornam a somatória e produtória de uma lista:

sum [1..10]
product [1..10]

Saída:


55
3628800

Quais tipos de lista são aceitos pelas funções sum e product?

3.12 Concatenando listas

Utilizamos o operador ++ para concatenar duas listas

[1..3] ++ [4..10] == [1..10]

Saída:


True

E o operador cons : adicionar um valor ao começo da lista:

1 : [2..10] == [1..10]

Saída:


True

Atenção à complexidade do operador ++

3.13 Exercício 8

Implemente a função fatorial utilizando o que aprendemos até agora.

3.14 Exercício 8 - Solução

Implemente a função fatorial utilizando o que aprendemos até agora.

fatorial n = product [1..n]

4 Pattern Matching com Listas

Quais padrões podemos capturar em uma lista?

Lista vazia:
- []
Lista com um elemento:
- (x : []) ou [x]
Lista com um elemento seguido de vários outros:
- (x : xs)

E qualquer um deles pode ser substituído pelo não importa _.

4.1 Implementando a função nulo

Para saber se uma lista está vazia utilizamos a função null:

null :: [a] -> Bool
null [] = True
null _  = False

4.2 Implementando a função tamanho

A função length pode ser implementada recursivamente da seguinte forma:

length :: [a] -> Int
length [] = 0
length (_:xs) = 1 + length xs

4.3 Exercício 9

Implemente a função take. Se n <= 0 deve retornar uma lista vazia.

4.4 Exercício 9 - Solução

Implemente a função take. Se n <= 0 deve retornar uma lista vazia.

take :: Int -> [a] -> [a]
take n _ | n <= 0 = []
take _ []         = []
take n (x:xs)     = x : take (n-1) xs

4.5 Strings

Assim como em outras linguagens, uma String no Haskell é uma lista de Char:

"Ola Mundo" == ['O','l','a',' ','M','u','n','d','o']

Saída:


True

5 Compreensão de Listas

Na matemática, quando falamos em conjuntos, definimos da seguinte forma:

\[ \{ x^2 \mid x \in \{1..5\} \} \]

que é lido como x ao quadrado para todo x do conjunto de um a cinco.

No Haskell podemos utilizar uma sintaxe parecida:

[x^2 | x <- [1..5]]

Saída:


[1,4,9,16,25]

que é lido como x ao quadrado tal que x vem da lista de valores de um a cinco.

A expressão x <- [1..5] é chamada de expressão geradora , pois ela gera valores na sequência conforme eles forem requisitados. Outros exemplos:

[toLower c | c <- "OLA MUNDO"]

Saída:


ola mundo

Ou ainda:

[(x, even x) | x <- [1,2,3]]

Saída:


[(1,False),(2,True),(3,False)]

Podemos combinar mais do que um gerador e, nesse caso, geramos uma lista da combinação dos valores deles:

[(x,y) | x <- [1..4], y <- [4..5]]

Saída:


[(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),(4,4),(4,5)]

Se invertermos a ordem dos geradores, geramos a mesma lista mas em ordem diferente:

[(x,y) | y <- [4..5], x <- [1..4]]

Saída:


[(1,4),(2,4),(3,4),(4,4),(1,5),(2,5),(3,5),(4,5)]

Isso é equivalente a um laço for encadeado!

Um gerador pode depender do valor gerado pelo gerador anterior:

[(i,j) | i <- [1..5], j <- [i+1..5]]

Saída:


[(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)]

Equivalente a:

for (i=1; i<=5; i++) {
  for (j=i+1; j<=5; j++) {
     // faça algo
  }
}

5.1 Exemplo: concat

A função concat transforma uma lista de listas em uma lista única concatenada (conhecido em outras linguagens como flatten):

concat [[1,2],[3,4]]

Saída:


[1,2,3,4]

Ela pode ser definida utilizando compreensão de listas:

concat xss = [x | xs <- xss, x <- xs]

5.2 Exercício 10 - `length`

Defina a função length utilizando compreensão de listas! Dica, você pode somar uma lista de 1s do mesmo tamanho da sua lista.

5.3 Exercício 10 - `length` - Solução

length xs = sum [1 | _ <- xs]

5.4 Guards

Nas compreensões de lista podemos utilizar o conceito de guardas para filtrar o conteúdo dos geradores condicionalmente:

[x | x <- [1..10], even x]

Saída:


[2,4,6,8,10]

5.5 Exemplo: Divisores

Vamos criar uma função chamada divisores que retorna uma lista de todos os divisores de n.

① Qual a assinatura?

divisores :: Int -> [Int]

② Quais os parâmetros?

divisores :: Int -> [Int]
divisores n = [???]

③ Qual o gerador?

divisores :: Int -> [Int]
divisores n = [x | x <- [1..n]]

④ Qual o guard?

divisores :: Int -> [Int]
divisores n = [x | x <- [1..n], n `mod` x == 0]

divisores 15

Saída:


[1,3,5,15]

5.6 Exercício 11

Utilizando a função divisores defina a função primo que retorna True se um certo número é primo.

5.7 Exercício 11 - Solução

primo :: Int -> Bool
primo n = divisores n == [1,n]

5.8 Primo

Note que para determinar se um número não é primo a função primo não vai gerar todos os divisores de n.

Por ser uma avaliação preguiçosa ela irá parar na primeira comparação que resultar em False:

primo 10 => 1 : _ == 1 : 10 : [] (1 == 1)
	 => 1 : 2 : _ == 1 : 10 : [] (2 /= 10)
	 False

Com a função primo podemos gerar a lista dos primos dentro de uma faixa de valores:

primos :: Int -> [Int]
primos n = [x | x <- [1..n], primo x]

primos 20 -- Os 20 primeiros primos

Saída:


[2,3,5,7,11,13,17,19]

Podemos ainda gerar a lista de todos os números primos. Lembre-se o Haskell vai na verdade criar uma promessa de lista que vai sendo gerada conforme necessário.

todosOsPrimos = [x | x <- [1..], primo x]

Pela natureza preguiçosa da linguagem ainda podemos, contudo, trabalhar com essa lista infinita. Por exemplo, para pegar o \(n-\text{ésimo}\) primo podemos usar a lista infinita. Lembre-se, a lista é indexada a partir de zero, então o \(n-\text{ésimo}\) elemento está na posição \(n - 1\).

nEsimoPrimo n = todosOsPrimos !! (n - 1)

nEsimoPrimo 1000 -- Milésimo primo

Saída:

5.9 A função `zip`

A função zip junta duas listas retornando uma lista de pares:

zip [1,2,3] [4,5,6]
zip [1,2,3] ['a', 'b', 'c']
zip [1,2,3] ['a', 'b', 'c', 'd']

Saída:


[(1,4),(2,5),(3,6)]
[(1,'a'),(2,'b'),(3,'c')]
[(1,'a'),(2,'b'),(3,'c')]

5.10 Função `pairs`

Vamos criar uma função que, dada uma lista, retorna os pares dos elementos adjacentes dessa lista, ou seja:

pairs [1,2,3]

Saída:


[(1,2),(2,3)]

A assinatura será:

pairs :: [a] -> [(a,a)]

E a definição será:

pairs :: [a] -> [(a,a)]
pairs xs = zip xs (tail xs)

5.11 Função `and`

A função and recebe uma lista de Bool e devolve True se todos os elementos são True e False caso contrário.

and :: [Bool] -> Bool
and []        = True
and (True:xs) = and xs
and _         = False

Também existe a função or que devolve verdadeiro se ao menos um dos elementos da lista for verdadeiro.

5.12 Exercício 12

Utilizando a função pairs defina a função sorted que retorna verdadeiro se uma lista está ordenada. Utilize também a função and que retorna verdadeiro se todos os elementos da lista forem verdadeiros.

sorted :: Ord a => [a] -> Bool

5.13 Exercício 12 - Solução

sorted :: Ord a => [a] -> Bool
sorted xs = and [x <= y | (x, y) <- pairs xs]

5.14 Para saber mais

Listas
Livros [GH] 5; [SGS] 2; [ML] 2

6 Recursão

Vejamos o que o Google tem a dizer a respeito disso…

A recursividade permite expressar ideias declarativas.
Composta por um ou mais casos bases (para que ela termine) e a chamada recursiva.

\[ n! = n . (n-1)! \]

Caso base:

\[ 1! = 0! = 1 \]

Para \(n = 3\):

3! = 3 . 2! = 3 . 2 . 1! = 3 . 2 . 1 = 6

fatorial :: Integer -> Integer
fatorial 0 = 1
fatorial 1 = 1
fatorial n = n * fatorial (n-1)

Casos bases primeiro!!

O Haskell avalia as expressões por substituição:

> fatorial 4
      => 4 * fatorial 3
      => 4 * (3 * fatorial 2)
      => 4 * (3 * (2 * fatorial 1))
      => 4 * (3 * (2 * 1))
      => 4 * (3 * 2)
      => 4 * 6
      => 24

Ao contrário de outras linguagens, ela não armazena o estado da chamada recursiva em uma pilha, o que evita o estouro da pilha.

A pilha recursiva do Haskell é a expressão armazenada, ele mantém uma pilha de expressão com a expressão atual. Essa pilha aumenta conforme a expressão expande, e diminui conforme uma operação é avaliada.

6.1 Máximo Divisor Comum

O algoritmo de Euclides para encontrar o Máximo Divisor Comum (greatest common divisor - gcd) é definido matematicamente como:

gcd :: Int -> Int -> Int
gcd 0 b = b
gcd a 0 = a
gcd a b = gcd b (a `rem` b)

> gcd 48 18
    => gcd 18 12
    => gcd 12 6
    => gcd 6 0
    => 6

Note que a pilha tem tamanho constante.
Em outras linguagens isto é chamado de recursão de cauda (_en: tail recursion _).

7 Recursão em Listas

Podemos também fazer chamadas recursivas em listas, de tal forma a trabalhar com apenas parte dos elementos em cada chamada:

sum :: Num a => [a] -> a
sum [] = 0
sum ns = ???

Preenchendo o corpo nós chegamos a:

sum :: Num a => [a] -> a
sum [] = 0
sum ns = (head ns) + sum (tail ns)

Por que não usar Pattern Matching?

sum :: Num a => [a] -> a
sum []     = 0
sum (n:ns) = n + sum ns

7.1 Exercício 13

Faça a versão caudal dessa função:

sum :: Num a => [a] -> a
sum []     = 0
sum (n:ns) = n + sum ns

7.2 Exercício 13 - Solução

Faça a versão caudal dessa função:

sum :: Num a => [a] -> a
sum [] = 0
sum ns = sum' ns 0
  where
    sum' [] s     = s
    sum' (n:ns) s = sum' ns (n+s)

7.3 Produtória

Como ficaria a função product baseado na função sum?

sum :: Num a => [a] -> a
sum []     = 0
sum (n:ns) = n + sum ns

① Alteramos o nome

product :: Num a => [a] -> a
product []     = 0
product (n:ns) = n + sum ns

② Alteramos a chamada recursiva

product :: Num a => [a] -> a
product []     = 1
product (n:ns) = n * product ns

7.4 Tamanho

E a função length?

sum :: Num a => [a] -> a
sum []     = 0
sum (n:ns) = n + sum ns

① Alteramos o nome

② Alteramos a chamada recursiva

length :: [a] -> Int
length []     = 0
length (n:ns) = 1 + length ns

Padrões de Programação

Reparem que muitas soluções recursivas (principalmente com listas) seguem um mesmo esqueleto. Uma vez que vocês dominem esses padrões, fica fácil determinar uma solução.
Em breve vamos criar funções que generalizam tais padrões.

7.5 Exercício 14

Crie uma função recursiva chamada insert que insere um valor x em uma lista ys ordenada de tal forma a mantê-la ordenada:

insert :: Ord a => a -> [a] -> [a]

7.6 Exercício 14 - Resposta

insert :: Ord a => a -> [a] -> [a]
insert x [] = [x]
insert x (y:ys) | x <= y    = x:y:ys
		| otherwise = y : insert x ys

7.7 Exercício 15

Crie uma função recursiva chamada isort que utiliza a função insert para implementar o Insertion Sort:

isort :: Ord a => [a] -> [a]

7.8 Exercício 15 - Resposta

isort :: Ord a => [a] -> [a]
isort []     = []
isort (x:xs) = insert x (isort xs)

7.9 Recursão Múltipla

Em alguns casos o retorno da função recursiva é a chamada dela mesma múltiplas vezes:

fib :: Int -> Int
fib 0 = 1
fib 1 = 1
fib n = fib (n-1) + fib (n-2)

7.10 Exercício 16

Complete a função qsort que implementa o algoritmo Quicksort:

qsort :: Ord a => [a] -> [a]
qsort []     = []
qsort (x:xs) = qsort menores ++ [x] ++ qsort maiores
  where
    menores = [a | ???]
    maiores = [b | ???]

7.11 Exercício 16 - Resposta

Complete a função qsort que implementa o algoritmo Quicksort:

qsort :: Ord a => [a] -> [a]
qsort []     = []
qsort (x:xs) = qsort menores ++ [x] ++ qsort maiores
  where
    menores = [a | a <- xs, a <= x]
    maiores = [b | b <- xs, b > x]

7.12 Para saber mais

Recursão
- Exercícios
Livros [GH] 6; [SGS] 2; [ML] 5
Livros [GH] 5; [SGS] 2; [ML] 2

8 Experimente tudo no Repl.it!

Código no Repl.it

9 Dicas finais sobre recursão

Vamos considerar a função drop que remove os n primeiros elementos de uma lista:

> drop 3 [1..10]
[4,5,6,7,8,9,10]

Passo 1: defina a assinatura da função

A função drop recebe um Int e uma lista e retorna outra lista, sem restrições:

drop :: Int -> [a] -> [a]

Passo 2: enumere os casos

Para o primeiro argumento da função, podemos ter o caso trivial 0 que não faz nada e o caso genérico n.

O segundo argumento pode ter a lista vazia [] e o caso genérico (x:xs). Vamos criar as combinações desses casos:

drop :: Int -> [a] -> [a]
drop 0 []     =
drop 0 (x:xs) =
drop n []     =
drop n (x:xs) =

Passo 3: defina os casos simples

Se eu não quero remover nada, retorno a própria lista, se eu quero remover algo de uma lista vazia, o retorno é vazio:

drop :: Int -> [a] -> [a]
drop 0 []     = []
drop 0 (x:xs) = x:xs
drop n []     = []
drop n (x:xs) =

Passo 4: defina os casos restantes

Como remover o primeiro elemento de (x:xs)? Removendo x e retornando apenas xs.

drop :: Int -> [a] -> [a]
drop 0 []     = []
drop 0 (x:xs) = x:xs
drop n []     = []
drop n (x:xs) = drop (n-1) xs

Passo 5: generalize e simplifique

O primeiro e terceiro caso são redundantes, o segundo caso não precisa de pattern matching na lista:

drop :: Int -> [a] -> [a]
drop _ []     = []
drop 0 xs     = xs
drop n (x:xs) = drop (n-1) xs

9.1 Exemplo - Cálculo de potências

Suponha que temos que calcular \(x^n\) para \(n\) inteiro positivo.
Como calcular de forma recursiva?

\(x^n\) é:

1, se \(n=0\).
\(x x^{n-1}\), caso contrário.

Defina a assinatura da função
Enumere os casos
Defina os casos simples
Defina os casos restantes
Simplifique

Vamos colocar a ideia em prática!

Defina a assinatura da função
Enumere os casos
Defina os casos simples
Defina os casos restantes
Simplifique

pot :: (Num a, Integral b) => a -> b -> a

Defina a assinatura da função ✓
Enumere os casos
Defina os casos simples
Defina os casos restantes
Simplifique

pot :: (Num a, Integral b) => a -> b -> a
pot b 0 =
pot b 1 =
pot b e =

Defina a assinatura da função ✓
Enumere os casos ✓
Defina os casos simples
Defina os casos restantes
Simplifique

pot :: (Num a, Integral b) => a -> b -> a
pot b 0 = 1
pot b 1 = b
pot b e =

Defina a assinatura da função ✓
Enumere os casos ✓
Defina os casos simples ✓
Defina os casos restantes
Simplifique

pot :: (Num a, Integral b) => a -> b -> a
pot b 0 = 1
pot b 1 = b
pot b e = b * pot b (e - 1)

Defina a assinatura da função ✓
Enumere os casos ✓
Defina os casos simples ✓
Defina os casos restantes ✓
Simplifique

pot :: (Num a, Integral b) => a -> b -> a
pot _ 0 = 1
pot b e = b * pot b (e - 1)

Daria para melhorar?

Podemos fazer uma versão com recursão de cauda (tente fazer por conta própria!). Mas tem outra saída melhor ainda…

E se definirmos a potência de forma diferente?

\(x^n\) é:

se \(n=0\), então \(x^n = 1\).
se \(n > 0\) e \(n\) é par, então \(x^n = (x^{n/2})^2\).
se \(n > 0\) e \(n\) é ímpar, então \(x^n = x(x^{(n-1)/2})^2\).

Note que aqui também definimos a solução do caso maior em termos de casos menores.

pot :: (Num a, Integral b) => a -> b -> a
pot _ 0 = 1
pot b e
  | even e     = aux * aux
  | otherwise  = b * aux * aux
  where
    aux = pot b (e `div` 2)

O algoritmo acima é mais eficiente que o anterior. Por quê?

9.2 Exemplo - Torres de Hanoi

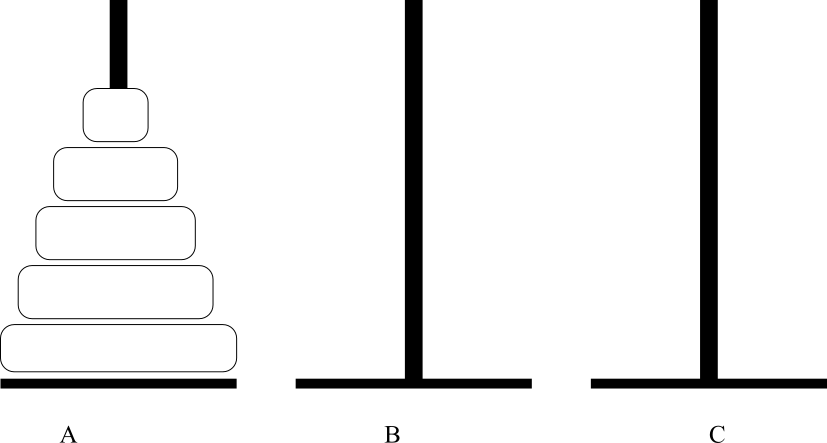
Inicialmente temos 5 discos de diâmetros diferentes na estaca A.
O problema das torres de Hanoi consiste em transferir os cinco discos da estaca A para a estaca C (pode-se usar a estaca B como auxiliar).
Porém deve-se respeitar as seguintes regras:
- Apenas o disco do topo de uma estaca pode ser movido.
- Nunca um disco de diâmetro maior pode ficar sobre um disco de diâmetro menor.

Vamos considerar o problema geral onde há \(n\) discos. Neste caso, vamos usar indução para obtermos um algoritmo para este problema.

Base: \(n=1\). Neste caso temos apenas um disco. Basta mover este disco da estaca A para a estaca C.
Hipótese: Sabemos como resolver o problema quando há \(n-1\) discos.
Passo: Devemos resolver o problema para \(n\) discos.
- Por hipótese de indução, sabemos mover os \(n-1\) primeiros discos da estaca A para B usando C} como auxiliar.
- Depois de movermos estes \(n-1\) discos, movemos o maior disco (que continua na estaca A) para a estaca C.
- Novamente pela hipótese de indução, sabemos mover os \(n-1\) discos da estaca B para C usando A como auxiliar.

Com isso temos uma solução para o caso onde há \(n\) discos. A indução nos fornece um algoritmo e ainda por cima temos uma demonstração formal de que ele funciona!

Problema: Mover \(n\) discos de A para C.

Se \(n=1\), então mova o único disco de A para C e pare.
Caso contrário (\(n > 1\)) desloque de forma recursiva os \(n-1\) primeiros discos de A para B, usando C como auxiliar.
Mova o último disco de A para C.
Mova, de forma recursiva, os \(n-1\) discos de B para C, usando A como auxiliar.

Escreva uma função com a assinatura abaixo que computa a solução para o problema

hanoi :: Int -> Char -> Char -> Char -> [(Int, Char, Char)]

A função recebe um inteiro representando o número de discos, e os idenficadores das estacas (ex. 'A', 'B' e 'C').
A sua função deve devolver uma lista com triplas onde o primeiro elemento é o disco a ser movido, o segundo a estaca de origem e o terceiro a estaca de destino

hanoi :: Int -> Char -> Char -> Char -> [(Int, Char, Char)]
hanoi 1 estacaInicio estacaFim _ =
  [(1, estacaInicio, estacaFim)]
hanoi n estacaInicio estacaFim estacaAux =
  hanoi (n - 1) estacaInicio estacaAux estacaFim ++
  [(n, estacaInicio, estacaFim)] ++
  hanoi (n - 1) estacaAux estacaFim  estacaInicio

Exercício: Faça uma versão que utilize uma variável acumuladora.

10 Disclaimer

Estes slides foram preparados para os cursos de Paradigmas de Programação e Desenvolvimento Orientado a Tipos na UFABC.

Este material pode ser usado livremente desde que sejam mantidos, além deste aviso, os créditos aos autores e instituições.

Conceitos Básicos - Parte 2

1 Polimorfismo

1.1 Overloaded types

1.2 Exemplos de funções

1.3 Exercício 1

1.4 Resposta 1

1.5 Cláusula where

1.6 Exercício 2

1.7 Resposta 2

1.8 Condicionais

1.9 Exercício 3

1.10 Resposta 3

1.11 Expressões guardadas (Guard Expressions)

1.12 Exercício 4

1.13 Resposta 4

1.14 Pattern Matching

1.15 Expressões \(\lambda\)

1.16 Operadores

1.17 Exercício 5

1.18 Resposta 5

1.19 Para saber mais

2 Listas

2.1 Criando listas

2.2 Para saber mais

3 Funções básicas para manipulação de listas

3.1 Recuperar elementos - !!

3.2 Recuperar elementos - head

3.3 Recuperar elementos - tail

3.4 Exercício 6

3.5 Exercício 6 - Solução

3.6 Recuperar elementos - take

3.7 Recuperar elementos - drop

3.8 Exercício 7

3.9 Exercício 7 - Solução

3.10 Tamanho da lista - length

3.11 Somatória e Produtória

3.12 Concatenando listas

3.13 Exercício 8

3.14 Exercício 8 - Solução

4 Pattern Matching com Listas

4.1 Implementando a função nulo

4.2 Implementando a função tamanho

4.3 Exercício 9

4.4 Exercício 9 - Solução

4.5 Strings

5 Compreensão de Listas

5.1 Exemplo: concat

5.2 Exercício 10 - length

5.3 Exercício 10 - length - Solução

5.4 Guards

5.5 Exemplo: Divisores

5.6 Exercício 11

5.7 Exercício 11 - Solução

5.8 Primo

5.9 A função zip

5.10 Função pairs

5.11 Função and

5.12 Exercício 12

5.13 Exercício 12 - Solução

5.14 Para saber mais

6 Recursão

6.1 Máximo Divisor Comum

7 Recursão em Listas

7.1 Exercício 13

7.2 Exercício 13 - Solução

7.3 Produtória

7.4 Tamanho

7.5 Exercício 14

7.6 Exercício 14 - Resposta

7.7 Exercício 15

7.8 Exercício 15 - Resposta

7.9 Recursão Múltipla

7.10 Exercício 16

7.11 Exercício 16 - Resposta

7.12 Para saber mais

8 Experimente tudo no Repl.it!

9 Dicas finais sobre recursão

9.1 Exemplo - Cálculo de potências

9.2 Exemplo - Torres de Hanoi

10 Disclaimer

3.1 Recuperar elementos - `!!`

3.2 Recuperar elementos - `head`

3.3 Recuperar elementos - `tail`

3.6 Recuperar elementos - `take`

3.7 Recuperar elementos - `drop`

3.10 Tamanho da lista - `length`

5.2 Exercício 10 - `length`

5.3 Exercício 10 - `length` - Solução

5.9 A função `zip`

5.10 Função `pairs`

5.11 Função `and`