Persistência
Playlists
- Desta aula: https://www.youtube.com/playlist?list=PLYItvall0TqIOxQzCMsK3zciIXxxgzlcG
- Do curso: https://www.youtube.com/playlist?list=PLYItvall0TqJ25sVTLcMhxsE0Hci58mpQ
1 Estruturas de dados persistentes
Uma propriedade que se torna evidente em estruturas de dados (EDs) funcionais é que elas são sempre persistentes
- Atualizações em uma ED não destroem a versão antiga.
- Elementos afetados são copiados.
- Elementos não afetados são compartilhados (en: shared) entre as diversas versões da ED.
1.1 Um primeiro exemplo: Listas
Listas são onipresentes em linguages funcionais e são expressas naturalmente em cálculo-\(\lambda\). As operações que elas dão suporte são normalmente as mesmas daquelas oferecidas por pilhas (en: stacks)
nova :: Pilha aCria uma nova pilha vaziavazia :: Pilha a -> BoolVerdadeiro se pilha vaziaempilha :: a -> Pilha a -> Pilha aEmpilha um valortopo :: Pilha a -> aRecupera o valor no topo da pilhadesempilha :: Pilha a -> Pilha aDesempilha um valor
-- Implementação na unha!
data Pilha a = Vazia | Cons a (Pilha a)
nova :: Pilha a
nova = Vazia
vazia :: Pilha a -> Bool
vazia Vazia = True
vazia _ = False
empilha :: a -> Pilha a -> Pilha a
empilha = Cons
topo :: Pilha a -> a
topo Vazia = error "Pilha vazia"
topo (Cons v _) = v
desempilha :: Pilha a -> Pilha a
desempilha Vazia = error "Pilha vazia"
desempilha (Cons _ p) = p
Ou, se utilizarmos as listas presentes por padrão em Haskell, teríamos:
type Pilha' a = [a]
nova' :: Pilha' a
nova' = []
vazia' :: Pilha' a -> Bool
vazia' = null
empilha' :: a -> Pilha' a -> Pilha' a
empilha' = (:)
topo' :: Pilha' a -> a
topo' = head
desempilha' :: Pilha' a -> Pilha' a
desempilha' = tail
A partir de agora, seja uma lista ou uma pilha, utilizaremos a nomenclatura tradicional de listas.
- Pilhas, de fato, são uma instância do caso mais geral de sequências. Outras instâncias que veremos durante o curso incluem: filas, filas de duas extremidades e listas catenárias.
Momento cultural
Concatenar tem a mesma raiz etimológica de catenária e ambas vêm
do latim catena: cadeia, corrente… Em inglês há inclusive o
verbo catenate equivalente ao nosso concatenar.
1.2 Catenárias…
-
Falando em catenária, outra operação comum em listas é a concatenação, normalmente representada pelo operador
(++). -
A concatenação de listas pode ser implementada facilmente em linguagens imperativas em tempo constante (\(O(1)\)).
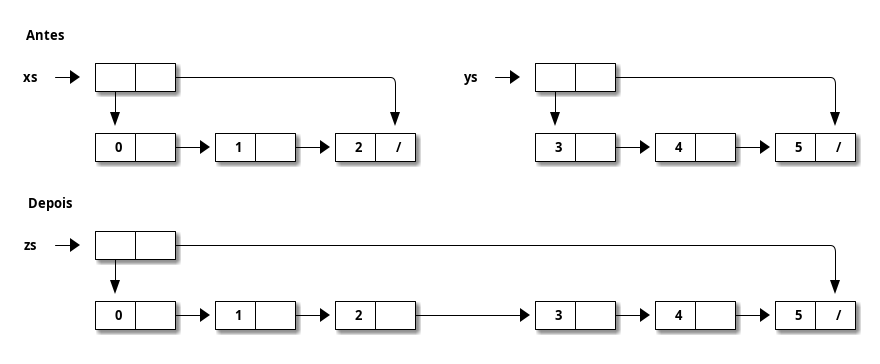
-
Porém, essa implementação imperativa é destrutiva em seus parâmetros. Após a execução de
(++), nemxsnemyspodem ser usadas novamente.- Não possui persistência.
-
Em uma linguagem funcional não há a possibilidade de fazer operações destrutivas, então a saída é fazer uma implementação que copia células, mantendo os valores e trocando o valor do apontador para a próxima célula.
- A implementação da operação
(++)fica:
(++) :: [a] -> [a] -> [a]
(++) [] ys = ys
(++) (x:xs) ys = x : (xs ++ ys)
A figura abaixo representa essa operação
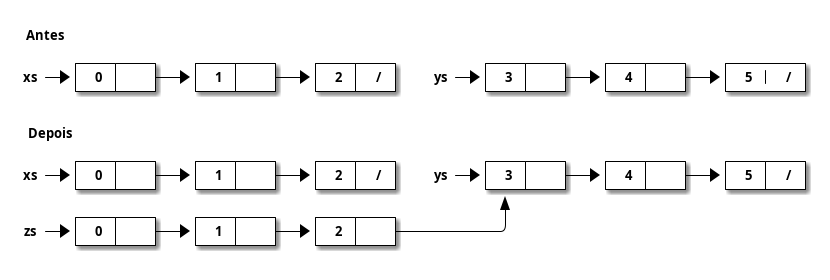
-
Ganhamos persistência, mas agora o custo passou a ser \(O(n)\) onde \(n\), é o comprimento de
xs.- Veremos mais adiante como reduzir esse custo para \(O(1)\).
-
Um caso parecido ocorre quando queremos fazer a atualização de um elemento com índice \(i\) da lista. Neste caso, precisamos copiar as células da lista ligada até o elemento desejado.
O código fica:
update :: [a] -> Int -> a -> [a]
update [] _ _ = error "Tentando atualizar lista vazia"
update (_:xs) 0 v = v:xs
update (x:xs) i v = x : update xs (i - 1) v
Graficamente ys = update xs 2 7:
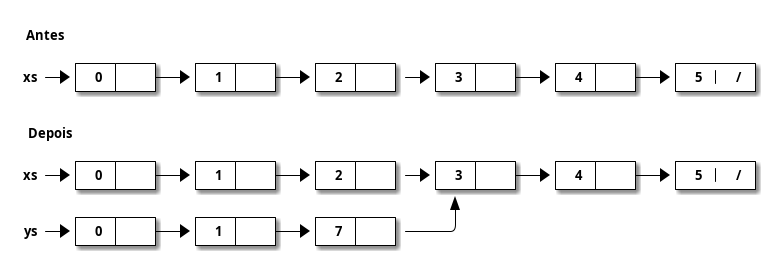
Apenas para reforçar: copiamos apenas o caminho até o elemento desejado.
Essa implementação se baseia fortemente no coletor de lixo (en: garbage collector). Implementar algo dessa maneira com controle de memória manual ficaria rapidamente complicadíssimo por conta dos compartilhamentos.
1.3 Exercício 1
- Escreva uma função
sufixos :: [a] -> [[a]]que recebe uma listaxse devolve uma lista com todos os sufixos da listaxsem ordem decrescente de comprimento. Por exemplo:sufixos [1, 2, 3, 4] = [[1,2,3,4],[2,3,4],[3,4],[4],[]] - Mostre que o resultado pode ser gerado em tempo \(O(n)\) e representado em espaço \(O(n)\).
1.4 Percorrendo listas
- Percorrer listas do início em direção ao fim é fácil e eficiente.
- Percorrer listas no sentido contrário é um pouco mais complicado.
- Uma lista em um contexto funcional é muito parecida com uma lista ligada com encadeamento simples utilizada corriqueiramente em linguagens imperativas.
1.5 Listas duplamente encadeadas - Tentativa de implementação
Como fazer uma lista duplamente encadeada caso queiramos percorrê-la em ambas as direções?
-- esquerda valor direita
data Lista2 a = Vazia2 | Cons2 (Lista2 a) a (Lista2 a)
null2 :: Lista2 a -> Bool
null2 Vazia2 = True
null2 _ = False
head2 :: Lista2 a -> a
head2 Vazia2 = error "Lista vazia"
head2 (Cons2 _ x _) = x
tail2 :: Lista2 a -> Lista2 a
tail2 Vazia2 = Vazia2
tail2 (Cons2 _ _ d) = d
Parece bom! Mas e agora, como implementar a função cons2?
cons2 :: a -> Lista2 a -> Lista2 a
cons2 = undefined -- ??
- O problema é que, agora, o nó seguinte da nossa lista aponta para o anterior. Modificar o nó inicial da lista causa uma alteração em cascata até o final da lista!
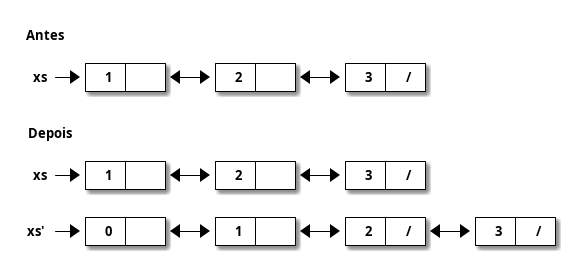
- Toda a lista precisa ser copiada! Não há compartilhamento!
- Colocar algo no fim da lista ou concatenar têm o mesmo problema.
- Temos o que queríamos, mas a que custo?

1.6 Zippers
Aqui veremos o uso aplicado de Zippers, mas existem maneiras formais de se definir um zipper para uma estrutura de dados qualquer. Na verdade um zipper é definido como a derivada da ADT[^fn:1]. Mais informações também podem ser vistas na aula sobre ADTs.
-
Zipper é um idiom (do inglês: expressão idiomática) de linguagens funcionais muito utilizado para manipular estruturas de dados persistentes.
-
Zippers podem ser usados não apenas para percorrer estruturas de dados como também para auxiliar em sua modificação.
Mas afinal, o que é um zipper?
Zippers funcionam de uma maneira parecida com aquela pela qual uma formiga explora o mundo.
- A localização atual da formiga é o foco do zipper.
- A formiga pode se deslocar para explorar o mundo seguindo os caminhos disponíveis.
- Para poder se orientar, ela deixa por cada local por onde passou uma trilha de feromônio que pode ser utilizada para retornar pelo mesmo caminho por onde ela veio.
- Esta última característica permite que implementemos, por exemplo, backtracking em linguagens funcionais de maneira eficiente.
- No caso específico de uma lista, a formiga/zipper, que mora em uma lista, explora um mundo unidimensional: ela só pode avançar ou retroceder.
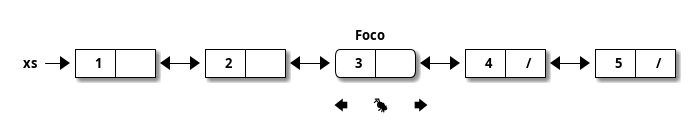
Como implementar tal abstração?
Simples! 2 listas!
- Uma contém o que ainda não foi percorrido da lista. Tudo à direita do foco.
- A outra contém uma trilha de migalhas, a trilha de feromônio da nossa formiga, para que ela possa voltar por onde veio. Tudo à esquerda do foco.
type ListZipper a = ([a], [a])
toListZipper :: [a] -> ListZipper a
toListZipper xs = ([], xs)
fromListZipper :: ListZipper a -> [a]
fromListZipper (es, ds) = reverse es ++ ds
lzFoco :: ListZipper a -> Maybe a
lzFoco (_, []) = Nothing
lzFoco (_, x:_) = Just x
lzDir :: ListZipper a -> Maybe (ListZipper a)
lzDir (_, []) = Nothing
lzDir (es, d:ds) = Just (d:es, ds)
lzEsq :: ListZipper a -> Maybe (ListZipper a)
lzEsq ([], _) = Nothing
lzEsq (e:es, ds) = Just (es, e:ds)
Tudo muito bem e muito bonito, mas além de percorrer a lista como uso isso para modificá-la?
- Imagine que temos uma lista de inteiros e queremos trocar todos
os números \(5\) por \(42\).
- Vamos definir, primeiramente, uma função para trocar o valor do elemento em foco.
lzTrocaFoco :: a -> ListZipper a -> Maybe (ListZipper a)
lzTrocaFoco _ (_, []) = Nothing
lzTrocaFoco y (es, _:ds) = Just (es, y:ds)
Agora podemos definir a função que troca os cincos:
trocaCincos :: [Int] -> [Int]
trocaCincos [] = []
trocaCincos xs =
fromListZipper $ trocaZip $ toListZipper xs
where
trocaZip z@(_, []) = z
trocaZip z@(_, d:_) =
let nz = if d == 5
then fromJust $ lzTrocaFoco 42 z
else z in
maybe nz trocaZip (lzDir nz)
-- Mas pra que tudo isso?
trocaCincos' :: [Int] -> [Int]
trocaCincos' xs = [if x == 5 then 42 else x | x <- xs]
1.7 Mas pra quê tudo isso?
Listas são estruturas de dados relativamente simples. Por isso a manipulação de um elemento é fácil…
- … e existem mecanismos como compreensão de listas que nos ajudam a fazer o que queremos.
Pense agora em estruturas um pouco mais elaboradas, como árvores ou grafos.
- O fato de estarmos lidando com uma linguagem funcional (e EDs persistentes) impede que simplesmente alteremos um valor de um nó na árvore através de um ponteiro!
- Precisamos substituir o nó que queremos modificar por um novo e “consertar” todo o caminho por onde passamos para que ele inclua as novas versões dos dados.
O caminho por onde passamos é justamente o caminho armazenado no Zipper!!
1.8 Exercício 2
Estude a função trocaCincos e as funções que ela utiliza. Em
seguida reimplemente a função fromListZipper :: ListZipper a -> [a].
Você não pode utilizar as funções (++) ou reverse (nem
reimplementá-las!).
trocaCincos :: [Int] -> [Int]
trocaCincos [] = []
trocaCincos xs =
fromListZipper $ trocaZip $ toListZipper xs
where
trocaZip z@(_, []) = z
trocaZip z@(_, d:_) =
let nz = if d == 5
then fromJust $ lzTrocaFoco 42 z
else z in
maybe nz trocaZip (lzDir nz)
2 Experimente no Repl.it
Experimente o código dessa seção no Repl.it abaixo:
3 Referências
3.1 Livros

- [CO]
- Purely Functional Data Structures
- Por Chris Okasaki

- [CLRS]
- Introduction to Algorithms
- Por Thomas H. Cormen & Charles E. Leiserson & Ronald L. Rives/t & /Clifford Stein

- [SW]
- Algorithms
- Por Robert Sedgewick & Kevin Wayne
3.2 Outras Referências
- Huet, Gérard. “The zipper.” Journal of functional programming 7.5 (1997): 549-554.
4 Disclaimer
Estes slides foram preparados para os cursos de Paradigmas de Programação e Desenvolvimento Orientado a Tipos na UFABC.
Este material pode ser usado livremente desde que sejam mantidos, além deste aviso, os créditos aos autores e instituições.
