Monads

Playlists

1 Monads

  • Vamos definir um tipo de dado que representa expressões matemáticas:
data Expr = Val Int
	  | Add Expr Expr
	  | Sub Expr Expr
	  | Mul Expr Expr
	  | Div Expr Expr
  • Para avaliar essa expressão podemos definir:
eval :: Expr -> Int
eval (Val n)   = n
eval (Add x y) = (eval x) + (eval y)
eval (Sub x y) = (eval x) - (eval y)
eval (Mul x y) = (eval x) * (eval y)
eval (Div x y) = (eval x) `div` (eval y)
  • Porém, se fizermos:
> eval (Div (Val 1) (Val 0))
*** Exception: divide by zero

1.1 Maybe

  • Podemos resolver isso usando maybeDiv e Maybe (vamos focar apenas na divisão):
eval :: Expr -> Maybe Int
eval (Val n)   = Just n
eval (Div x y) = case eval x of
		    Nothing -> Nothing
		    Just n  -> case eval y of
				  Nothing -> Nothing
				  Just m  -> maybeDiv n m
  • Agora temos:
> eval (Div (Val 1) (Val 0))
Nothing
  • Mas nosso código está confuso…
  • O uso de Applicative pode resolver muitos problemas de encadeamento de funções com efeito
  • Seria legal poder fazer:
pure maybeDiv <*> eval x <*> eval y
  • Mas maybeDiv tem tipo Int -> Int -> Maybe Int e deveria ser Int -> Int -> Int para o uso de applicativo.

  • O problema aqui é que o uso de Applicative é para sequências de computações que podem ter efeitos mas que são independentes entre si.

  • Queremos agora uma sequência de computações com efeito mas que uma computação dependa da anterior.

  • Precisamos de uma função que capture nosso padrão de case of:
vincular :: Maybe a -> (a -> Maybe b) -> Maybe b
vincular mx g = case mx of
		  Nothing -> Nothing
		  Just x  -> g x
  • O nome significa que estamos vinculando o resultado da computação de mx ao argumento da função g.
  • No Haskell esse operador é conhecido como bind e definido como:
(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b

  • Qualquer semelhança com o logo de Haskell, é mera coincidência 😄

1.2 Monoid de Monad

  • Em teoria das categorias um Monad pode ser visto como um Monoid das categorias dos Functors.
    • O elemento identidade é o return
    • O operador associativo é uma variação de (>>=) com a assinatura:
(>=>) ::Monad m=> (a -> m b) -> (b -> m c) -> (a -> m c)

Ou seja, duas funções que transformam um valor puro em um Monad podem ser combinadas formando uma terceira função.

(>=>) também chamado de operador peixe (_ fish operator_).

  • Com isso podemos reescrever eval como:
eval :: Expr -> Maybe Int
eval (Val n)   = Just n
eval (Div x y) = eval x >>= \n ->
		 eval y >>= \m ->
		 maybeDiv n m

> eval (Div (Val (Just 4)) (Val (Just 2)))
  => (Just 4) >>= \n ->
	      (Just 2) >>= \m -> maybeDiv n m
  => (Just 2) >>= \m -> maybeDiv 4 m
  => maybeDiv 4 2

> eval (Div (Val (Nothing)) (Val (Just 2)))
  => Nothing >>= \n ->
	     (Just 2) >>= \m -> maybeDiv n m
  => Nothing

> eval (Div (Val (Just 4)) (Val (Nothing))
  => (Just 4) >>= \n ->
	      (Just 2) >>= \m -> maybeDiv n m
	      => Nothing >>= \m -> maybeDiv 4 m
  => Nothing
  • Generalizando, uma expressão construída com o operador (>>=) tem a seguinte estrutura:
m1 >>= \x1 ->
m2 >>= \x2 ->
...
mn >>= \xn ->
f x1 x2 ... xn
  • Indicando um encadeamento de computação sequencial para chegar a uma aplicação de função. Esse operador garante que se uma computação falhar, ela para imediatamente e reporta a falha (em forma de Nothing, [], etc.)

1.3 Monads: Syntactic Sugar

  • Essa mesma expressão pode ser escrita com a notação chamada do-notation :
do x1 <- m1
   x2 <- m2
   ...
   xn <- mn
   f x1 x2 ... xn
  • Com isso podemos reescrever eval novamente como:
eval :: Expr -> Maybe Int
eval (Val n)   = Just n
eval (Div x y) = do n <- eval x
		    m <- eval y
		    safeDiv n m
  • Que captura uma sequência de computações que devem respeitar a ordem, são dependentes e podem falhar. Uma notação imperativa? 🤔
  • Esse tipo de operação forma uma nova classe de tipos denominada Monads :
class Applicative m => Monad m where
   return :: a -> m a
   (>>=)  :: m a -> (a -> m b) -> m b

   return = pure
  • Além do operador bind ela redefine a função pure com o nome de return.
  • Já escrevemos a definição de Monad Maybe mas podemos deixá-la mais clara utilizando Pattern Matching:
instance Monad Maybe where
   Nothing  >>= _ = Nothing
   (Just x) >>= f = f x

2 SafeNum + Monad

-- Versão com monad
f3' :: Int -> Int -> SafeNum Int
f3' x y =
  safeDiv x y >>= \xy ->
  safeDiv y x >>= \yx ->
  safeAdd xy yx

f3 :: Int -> Int -> SafeNum Int
f3 x y = do
  xy <- safeDiv x y
  yx <- safeDiv y x
  safeAdd xy yx

-- Versão "pura"
f0 :: Int -> Int -> SafeNum Int
f0 x y
  | isSafe xy && isSafe yx = safeAdd (unbox xy) (unbox yx)
  | (not.isSafe) xy = xy
  | otherwise = yx
  where
    xy = safeDiv x y
    yx = safeDiv y x
    unbox (SafeNum x) = x
    isSafe (SafeNum _) = True
    isSafe _           = False

-- Versão com functors
f1 :: Int -> Int -> SafeNum Int
f1 x y =
  let xy = safeDiv x y
      yx = safeDiv y x
      safeAddXY = fmap safeAdd xy
      safeXYPlusYX = fmap (`fmap` yx) safeAddXY
  in
    (flatten.flatten) safeXYPlusYX

-- Versão com applicative
f2 :: Int -> Int -> SafeNum Int
f2 x y =
  let xy = safeDiv x y
      yx = safeDiv y x
  in
    flatten $ pure safeAdd <*> xy <*> yx

-- Versão com monad
f3 :: Int -> Int -> SafeNum Int
f3 x y = do
  xy <- safeDiv x y
  yx <- safeDiv y x
  safeAdd xy yx

2.1 Exercício 1

  • Escreva a instância de Monad para o tipo SafeNum.
data SafeNum a = NaN | NegInf| PosInf | SafeNum a deriving Show

2.2 Resposta - Exercício 1

data SafeNum a = NaN | NegInf| PosInf | SafeNum a deriving Show

instance Monad SafeNum where
  (SafeNum v) >>= f = f v
  v           >>= _ = boxedCoerce v

3 Monads e Efeitos

  • Embora a linguagem Haskell seja conhecida como uma linguagem puramente funcional .

Existe um limite do quanto nosso programa pode ser puro!

  • Imagine um programa que computa 1 milhão de casas decimais de \(\pi\) só que não imprime o resultado por causa da ausência de efeitos colaterais.

As funções impuras são necessárias para diversas ocasiões conforme apontado por Eugenio Moggi:

  • Parcialidade
  • Não-determinismo
  • Efeitos colaterais: Read only, Write only, Read/Write
  • Exceções
  • Continuações
  • Entrada e Saída Interativa

3.1 Parcialidade

  • Quando temos uma função que pode não terminar.
  • Valor bottom ⊥:
f :: a -> Bool

retorna True, False ou _|_.

3.2 Não-determinismo

Quando uma função pode retornar diferentes saídas dependendo de certas condições internas ou externas, ela é dita não-determinística .

Por exemplo, ao jogar um dado, podemos ter seis saídas diferentes!

Uma forma de modelar não-determinismo é com uso de listas:

data Dado = Um | Dois | Tres | Quatro | Cinco | Seis
	       deriving (Show, Bounded, Enum, Eq)

jogaDado = [Um .. Seis]

A cada jogada de dados, eu recebo um novo número de Um a Seis. Quais combinações eu posso ter ao jogar os dados duas vezes?

jogaDuasVezes = do
  dado1 <- jogaDado
  dado2 <- jogaDado
  return (dado1, dado2)

jogaDuasVezes

Saída:


[(Um,Um),(Um,Dois),(Um,Tres),(Um,Quatro),(Um,Cinco),(Um,Seis),(Dois,Um),(Dois,Dois),(Dois,Tres),(Dois,Quatro),(Dois,Cinco),(Dois,Seis),(Tres,Um),(Tres,Dois),(Tres,Tres),(Tres,Quatro),(Tres,Cinco),(Tres,Seis),(Quatro,Um),(Quatro,Dois),(Quatro,Tres),(Quatro,Quatro),(Quatro,Cinco),(Quatro,Seis),(Cinco,Um),(Cinco,Dois),(Cinco,Tres),(Cinco,Quatro),(Cinco,Cinco),(Cinco,Seis),(Seis,Um),(Seis,Dois),(Seis,Tres),(Seis,Quatro),(Seis,Cinco),(Seis,Seis)]

Imagine agora que esse dado é mágico, e toda vez que ele cai em um número par, o próximo é ímpar e vice-versa:

magica :: Dado -> [Dado]
magica dado
  | any (dado==) [Um, Tres, Cinco] = [Dois, Quatro, Seis]
  | otherwise                      = [Um, Tres, Cinco]

jogaDuasVezes' :: [(Dado, Dado)]
jogaDuasVezes' = do
  dado1 <- jogaDado
  dado2 <- magica dado1
  return (dado1, dado2)

jogaDuasVezes'

Saída:


[(Um,Dois),(Um,Quatro),(Um,Seis),(Dois,Um),(Dois,Tres),(Dois,Cinco),(Tres,Dois),(Tres,Quatro),(Tres,Seis),(Quatro,Um),(Quatro,Tres),(Quatro,Cinco),(Cinco,Dois),(Cinco,Quatro),(Cinco,Seis),(Seis,Um),(Seis,Tres),(Seis,Cinco)]
  • A Monad lista é definida como:
instance Monad [] where
  xs >>= f = [y | x <- xs, y <- f x]

Nossa função jogaDuasVezes usando bind fica:

jogaDuasVezes :: [(Dado, Dado)]
jogaDuasVezes = jogaDado >>= \dado1 ->
		  jogaDado >>= \dado2 ->
		    return (dado1, dado2)

E a versão jogaDuasVezes' como:

jogaDuasVezes' :: [(Dado, Dado)]
jogaDuasVezes' = jogaDado >>= \dado1 ->
		  magica dado1 >>= \dado2 ->
		   return (dado1, dado2)
  • Para gerar todas as combinações de elementos de duas listas pode ser escrito como:
pares :: [a] -> [b] -> [(a,b)]
pares xs ys = xs >>= \x ->
	      ys >>= \y ->
	      return (x,y) -- [(x,y)]
  • Ou em do-notation:
pares :: [a] -> [b] -> [(a,b)]
pares xs ys = do x <- xs
		 y <- ys
		 return (x,y)

> pares [1,2] [3,4]
  => [1,2] >>= \x ->
	  [3,4] >>= \y ->
	       [(x,y)]
  => [x' | x  <- [1,2],
	   x' <- \x -> [3,4] >>= \y -> [(x,y)]]
  => [x' | x  <- [1,2],
	   x' <- \x -> [y' | y <- [3,4], y' <- [(x,y)]]
  => [x' | x  <- [1,2],
	   x' <- \x -> [y' | y' <- [(x,3), (x,4)]]
  => [x' | x  <- [1,2],
	   x' <- \x -> [(x,3), (x,4)]]
  => [x' | x' <- [(1,3),(1,4),(2,3),(2,4)]]
  => [(1,3),(1,4),(2,3),(2,4)]
  • A compreensão de listas surgiu a partir da notação do:
pares xs ys = [(x,y) | x <- xs, y <- ys]
  == do x <- xs
	y <- ys
	return (x,y)

3.3 Exceções: Either

  • Para lidarmos com funções parciais ou que geram

exceções, podemos utilizar o Maybe.

  • Porém, ele apenas indica que houve um problema

na avaliação das funções, mas não diz qual foi ele.

  • Um tipo que generaliza o Maybe e permite reportar

o ponto que ocorreu a falha é o Either:

data Either a b = Left a | Right b
  • Podemos definir Left como o log do erro e Right

como o valor esperado, caso tudo dê certo.

  • A instância de Functor age apenas no valor da direita:
instance Functor (Either a) where
  fmap f (Left x) = Left x
  fmap f (Right x) = Right (f x)
  • Similar ao Maybe, a instância de Applicative

propaga o Left e aplica a função no Right:

instance Applicative (Either a) where
  pure x = Right x

  (Left f)  <*> _         = Left f
  _         <*> (Left x)  = Left x
  (Right f) <*> (Right x) = Right (f x)
  • A instância de Monad também é similar ao Maybe:
instance Monad (Either a) where
  (Left x) >>= f  = Left x
  (Right x) >>= f = f x
  • Com isso podemos fazer:
safeDiv :: (Show a, Eq a, Floating a) => a -> a -> Either String a
safeDiv a b
  | b == 0 = Left ("Divisao por zero: " ++ show a ++ "/" ++ show b)
  | otherwise = Right (a/b)

safeLog :: (Show a, Ord a, Eq a, Floating a) => a -> Either String a
safeLog x
  | x <= 0    = Left ("Log invalido: " ++ show x)
  | otherwise = Right (log x)

safeAdd :: Floating a => a -> a -> Either String a
safeAdd a b = Right (a+b)

safeExpr1, safeExpr2 :: Either String Double
safeExpr1 = do q <- safeDiv 10 (-2)
	       l <- safeLog q
	       safeAdd 2 q

safeExpr2 = do q <- safeDiv 10 0
	       safeAdd 2 q

print safeExpr1
print safeExpr2

3.4 Experiment no Repl.it

Código no Repl.it

3.5 Efeitos Colaterais: Read Only

  • Digamos que temos uma configuração global compartilhada com todas as funções:
data Config = Conf { tweet_key  :: String
		   , api_secret :: String
		   }

E toda função f :: a -> b passa a receber um argumento adicional Config com essa configuração global:

postTweet :: (String, Config) -> String
postTweet (t, e)
  | valida (t, e) = t
  | otherwise     = "senha inválida"

valida :: (String, Config) -> Bool
valida (x, e)
  | (tweet_key e) == "teste" = True
  | otherwise = False
  • Veja que essencialmente postTweet, valida tem tipos String -> () e String -> Bool, mas foram embelezadas para receber também as configurações globais.
  • Aplicando currying temos:
postTweet :: String -> Config -> String
postTweet t e
  | valida t e = t
  | otherwise  = "senha inválida"

valida :: String -> Config -> Bool
valida x e
  | (tweet_key e) == "teste" = True
  | otherwise = False
  • E podemos definir o tipo:
data Reader e a = Reader (e -> a)

postTweet :: String -> Reader Config ()
valida :: String -> Reader Config Bool
  • Como fica a instância de Functor para o tipo Reader?
data Reader e a = Reader (e -> a)

instance Functor (Reader e) where
  -- fmap :: (a -> b) -> Reader e a -> Reader e b
  fmap f (Reader g) = Reader (f.g)
  • E a instância de Applicative?
data Reader e a = Reader (e -> a)

runReader :: Reader e a -> e -> a
runReader (Reader f) e = f e

instance Applicative (Reader e) where
  -- pure :: a -> Reader e a
  pure x = Reader (\e -> x)

  -- (<*>) :: Reader e (a -> b) -> Reader e a -> Reader e b
  rab <*> ra = Reader (\e -> ab e (a e))
    where
      ab = runReader rab -- :: e -> (a -> b)
      a  = runReader ra  -- :: e -> a
  • Para evitar os parênteses, podemos reescrever como:
instance Applicative (Reader e) where
  -- pure :: a -> Reader e a
  pure x = Reader (\e -> x)

  -- (<*>) :: Reader e (a -> b) -> Reader e a -> Reader e b
  rab <*> ra = Reader (\e -> let fab = runReader rab e
				 fa  = runReader ra e
			     in  fab fa)
  • Finalmente para criar a instância de Monad temos:
data Reader e a = Reader (e -> a)

instance Monad (Reader e) where
  -- (>>=) :: Reader e a -> (a -> Reader e b) -> Reader e b
  ra >>= arb =
    Reader (\e -> let a  = runReader ra e -- a
		      rb = arb a -- Reader e b
		  in  runReader rb e)
  • Uma versão simplificada do exemplo do tweet acima fica:
postTweet :: String -> Reader Config String
postTweet t = do
  b <- valida t
  if b then return t
  else return "senha inválida"

valida :: String -> Reader Config Bool
valida x = do
  key <- askfor tweet_key
  if key == "teste"
  then return True
  else return False

3.6 Experiment no Repl.it

Código no Repl.it

3.7 Efeitos Colaterais: Write Only

  • Considere o seguinte código:
isEven x = even x
not'   b = not b
isOdd  x = (not' . isEven) x
  • Digamos que eu gostaria de gravar o traço de execução para verificar as funções que são chamadas. Logo eu gostaria que:
> isOdd 3
(True, " isEven not' ")
  • Podemos criar novas versões de nossas funções:
isEven x = (even x, " isEven ")
not'   b = (not b, " not' ")
isOdd  x = (not' . isEven) x -- ops
  • Não é mais possível compor as funções isEven e not'…
isEven x = (even x, " isEven ")
not'   b = (not b, " not' ")
isOdd  x = let (b1, trace1) = isEven x
	       (b2, trace2) = not' b
	   in  (b2, trace1 ++ trace2)
  • Nada prático…
  • As assinaturas dessas funções seguem o formato a -> (b, String):
isEven :: Integer -> (Bool, String)
isEven x = (even x, " isEven ")

not' :: Bool -> (Bool, String)
not'   b = (not b, " not' ")

isOdd :: Integer -> (Bool, String)
isOdd  x = let (b1, trace1) = isEven x
	       (b2, trace2) = not' b
	   in  (b2, trace1 ++ trace2)
  • Fazendo m = (, String), temos a -> m b 🤔
  • Vamos definir o tipo Writer e algumas funções auxiliares:
data Writer w a = Writer a w

runWriter :: Writer w a -> (a, w)
runWriter (Writer a w) = (a, w)

tell :: w -> Writer w ()
tell s = Writer () s

O w do tipo Writer representa o tipo do efeito colateral desejado, no nosso exemplo, a String.

  • A instância de Functor simplesmente aplica uma função no valor sem causar um efeito colateral.
instance (Monoid w) => Functor (Writer w) where
  -- fmap :: (a -> b) -> Writer w a -> Writer w b
  fmap f (Writer a w) = Writer (f a) w

Hmmm…Monoid 🤔

  • Para a instância de Applicative a função pure cria um valor sem efeito colateral. No nosso exemplo, a String vazia! O operador aplicar simplesmente aplica a função no valor e concatena os efeitos!
instance (Monoid w) => Applicative (Writer w) where
  -- pure :: a -> Writer w a
  pure x = Writer x mempty

  -- (<*>) :: Writer w (a -> b) -> Writer w a -> Writer w b
  (Writer f m1) <*> (Writer a m2) = Writer (f a) (m1 <> m2)
  • A instâcia de Monad aplica a função no valor puro de

nosso Writer, gerando um efeito colateral…

instance (Monoid w) => Monad (Writer w) where
  -- (Writer w a) -> (a -> Writer w b) -> (Writer w b)
  (Writer a w) >>= k = let (b, w') = runWriter (k a)
		       in  Writer b (w <> w')

…em seguida retorna o valor com os efeitos compostos.

  • Dessa forma nosso exemplo fica:
isEvenW' :: Integer -> Writer String Bool
isEvenW' x = do tell " even "
		return (even x)

notW' :: Bool -> Writer String Bool
notW' b = do tell " not "
	     return (not b)
  • E podemos definir isOddW' com o operador

de composição de Monads >=>:

-- (>=>) :: (a -> m b) -> (b -> m c) -> (a -> m c)
isOddW' :: Integer -> Writer String Bool
isOddW' = (isEvenW' >=> notW')

3.8 Experiment no Repl.it

Código no Repl.it

3.9 Efeitos Colaterais: Read and Write

  • Considere o seguinte problema: tenho uma árvore do tipo Tree Char e quero converter para uma Tree Int sendo que os nós folhas receberão números de [0..] na sequência de visita:
data Tree a = Leaf a | Node (Tree a) (Tree a)
	      deriving Show

tree :: Tree Char
tree = Node (Node (Leaf 'a') (Leaf 'b')) (Leaf 'c')

f tree = Node (Node (Leaf 0) (Leaf 1)) (Leaf 2)

3.10 Estado

Um esqueleto dessa função seria:

data Tree a = Leaf a | Node (Tree a) (Tree a)
	      deriving Show

rlabel :: Tree a -> Tree Int
rlabel (Leaf _)   = Leaf n
rlabel (Node l r) = Node (rlabel l) (rlabel r)

  • Queremos que n seja uma variável de estado, ou seja, toda vez que a utilizarmos ela altere seu estado!

  • Mas somos puros e imutáveis! Como podemos resolver isso?

  • Uma ideia é incorporar o estado atual na declaração da função:
rlabel :: Tree a -> Int -> (Tree Int, Int)
rlabel (Leaf _) n = (Leaf n, n + 1)
rlabel (Node l r) = (Node l' r', n'')
  where
    (l', n')   = rlabel l n  -- altera o estado de n
    (l'', n'') = rlabel r n' -- altera o estado de n'

Com isso podemos chamar:

> rlabel tree 0
 => (Node l' r', n'')
> (l', n') = rlabel (Node (Leaf 'a') (Leaf 'b')) 0
 => (Node l' r', n'')
> (l', n') = rlabel (Leaf 'a') 0
  => (Leaf 0, 1)
> (r', n'') = rlabel (Leaf 'b') 1
 => (Leaf 1, 2)
> (r, n'') = rlabel (Leaf 'c') 2
 => (Leaf 2, 3)

(Node (Node (Leaf 0) (Leaf 1)) (Leaf 2), 3)
  • Vamos generalizar o tipo Tree a -> Int -> (Tree Int, Int)
t -> (a -> (b, a))
  • A segunda parte me lembra algo…🤔
  • O tipo Reader é a -> b, o tipo Writer é (a, b):
t -> (a -> (b, a))
t -> Reader a (Writer a b)
  • Faz sentido, queremos um valor que pode ser lido e alterado: Reader-Writer.

3.11 Transformador de Estado

  • Vamos definir o tipo State como:
--             = Reader s (Writer s a)
data State s a = State (s -> (a, s))

Com isso a assinatura de rlabel pode se tornar:

rlabel :: Tree a -> State Int (Tree Int)
  • Um transformador de estado pode ser visto como uma caixa que recebe um estado e retorna um valor e um novo estado:
Figure 1: Transformador de estado

Figure 1: Transformador de estado

  • Podemos pensar também em um transformador de estados que, além de um estado, recebe um valor para agir dentro do ambiente que ele vive:
Figure 2: Transformador de estado

Figure 2: Transformador de estado

  • Vamos criar uma função auxiliar para aplicar um transformador de estado em um estado (que está encapsulado no construtor State):
runState :: State s a -> s -> (a, s)
runState (State f) s = f s

Essencialmente, as instâncias de Functor, Applicative, Monad são muito parecidas com as do Reader.

  • A ideia geral de um Functor ST é que ele defina como aplicar uma função pura do tipo a -> b na parte do valor do resultado de um ST a, transformando-o efetivamente em um tipo ST b:
Figure 3: Functor ST

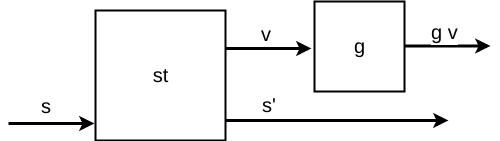
Figure 3: Functor ST

Com isso temos:

instance Functor (State s) where
  -- fmap :: (a -> b) -> State s a -> State s b
  fmap f (State g) = State (\s -> let (a, s') = g s
				  in  (f a, s'))
  • criamos uma função que gera o valor a e um novo estado e, então, retorna f a com esse novo estado.

  • Esse Functor promete aplicar uma função pura apenas no valor de saída do transformador de estado, sem influenciar o estado.

  • Se em rlabel eu quiser gerar rótulos pares, poderia aplicar fmap (*2) a função de estado.

  • A classe Applicative define formas de combinar computações sequenciais puras dentro de computações que podem sofrer efeitos colaterais.

  • Embora cada computação na sequência possa alterar o estado s, o valor final é a computação dos valores puros.

A definição de pure cria um transformador de estado puro, ou seja, que não altera o estado:

Figure 4: pure ST

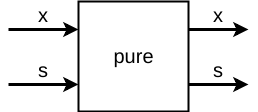
Figure 4: pure ST

Então definimos:

instance Applicative (State s) where
  -- pure :: a -> State s a
  pure x = State (\s -> (x, s))
  • A definição do operador (<*>) define a sequência de mudança de estados pelos transformadores e a combinação dos valores finais como um resultado único:
Figure 5: &lt;*&gt; ST

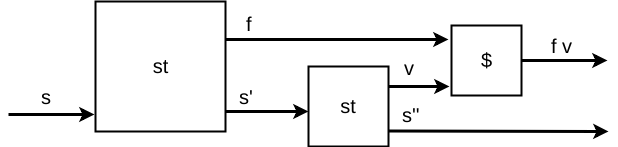
Figure 5: <*> ST

Então definimos:

instance Applicative (State s) where
  -- (<*>) :: State s (a -> b) -> State s a -> State s b
  sab <*> sa = State (\s -> let (f, s1) = runState sab s
				(a, s2) = runState sa  s1
			    in  (f a, s2))

Como primeiro passo é preciso recuperar a função f, o que altera o estado. Em seguida, recuperamos a utilizando o novo estado, gerando o próximo estado. Finalmente, aplicamos f a e retornamos o último estado gerado.

No nosso exemplo de rlabel, podemos imaginar algo como:

pure Leaf <*> sInc
  • Se sInc é um transformador de estados que incrementa um contador, então:
    1. pure Leaf é aplicado no estado atual s retornando ele mesmo (pois é puro)
    2. sInc é aplicado a s retornando um novo estado com o contador incrementado: (Leaf n, n + 1)

No caso de Monads, queremos definir um operador (>>=) que se comporte como:

Figure 6: Monad ST

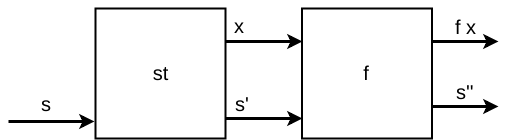
Figure 6: Monad ST

  • Podemos observar que o operador bind age de forma similar a (<*>), porém cada encadeamento gera um novo transformador de estado que pode depender do valor retornado pelo transformador anterior.

  • Ou seja, um Monad ST pode ser usado quando queremos gerar novos transformadores dependendo do valor de retorno de outro.

Com isso definimos:

instance Monad (State s) where
  -- (>>=) :: State s a -> (a -> State s b) -> State s b
  sa >>= f = State (\s -> let (a, s1) = runState sa s
			      sb      = f a
			  in  runState sb s1)

Primeiro recuperamos o valor de a, gerando um novo estado. Em seguida, aplicamos f a que gera um novo State que é executado com o último estado gerado.

No nosso exemplo de rlabel, podemos imaginar algo como:

do n <- sInc
   return (Leaf n)

para alterar o rótulo de um nó folha.

3.12 Applicative rlabel

data Tree a = Leaf a | Node (Tree a) (Tree a)
	      deriving Show

rlabel :: Tree a -> Int -> (Tree Int, Int)
rlabel (Leaf _) n   = (Leaf n, n+1)
rlabel (Node l r) n = let (l', n1) = rlabel l n
			  (r', n2) = rlabel r n1
		      in  (Node l' r', n2)

A versão completa do Applicative rlabel fica:

alabel :: Tree a -> State Int (Tree Int)
alabel (Leaf _) = pure Leaf <*> sInc
alabel (Node l r) = pure Node <*> alabel l <*> alabel r

mlabel :: Tree a -> State Int (Tree Int)
mlabel (Leaf _) = do n <- sInc
		     return (Leaf n)
mlabel (Node l r) = do l' <- mlabel l
		       r' <- mlabel r -- e se eu trocar a ordem?
		       return $ Node l' r'

Finalmente, a definição de sInc fica:

sInc :: State Int Int
sInc = S (\n -> (n, n+1))

3.13 Experiment no Repl.it

Código no Repl.it

Para aplicar essas funções, devemos fazer:

tree :: Tree Char
tree = Node (Node (Leaf 'a') (Leaf 'b')) (Leaf 'c')

newtype ST a = S (State -> (a, State))
app :: ST a -> State -> (a, State)
app (S st) s = st s

sInc :: ST Int
sInc = S (\n -> (n, n+1))

alabel :: Tree a -> ST (Tree Int)
alabel (Leaf _)   = pure Leaf <*> sInc
alabel (Node l r) = pure Node <*> alabel l <*> alabel r

> stTree = alabel tree -- cria transformador de estado
> app stTree 0         -- começa a contar do 0
(Node (Node (Leaf 0) (Leaf 1)) (Leaf 2), 3)

3.14 Efeitos Colaterais: IO

  • Conforme discutimos anteriormente, funções de entrada e saída de dados são impuras pois alteram o estado atual do sistema.

  • A função getChar captura um caracter do teclado. Se eu executar tal função duas vezes, o valor da função não necessariamente será igual.

  • A função putChar escreve um caracter na saída padarão (ex.: monitor). Se eu executar duas vezes seguidas com a mesma entrada, a saída será diferente.

Basicamente, as funções de entrada e saída alteram estado, ou seja:

newtype IO a = newtype ST a = State -> (a, State)

com a definição de estado sendo:

type State = Environment

o estado sendo o ambiente, sistema operacional, o mundo computacional que ele vive.

Com isso, tudo que fizemos até agora é suficiente para trabalharmos com IO sem afetar a pureza dos nossos programas:

getchar :: IO Char

putChar :: Char -> IO ()

Se eu fizer:

do putChar 'a'
   putChar 'a'

Na verdade ele estará fazendo algo como:

(_, env')  = putChar 'a' env
(_, env'') = putChar 'a' env'

  • No Haskell chamamos as funções de entrada e saída como ações de IO (_ IO actions _).

  • As funções básicas são implementadas internamente de acordo com o Sistema Operacional

Vamos trabalhar inicialmente com três ações básicas:

-- recebe um caracter da entrada padrão
getChar :: IO Char

-- escreve um caracter na saída padrão
putChar :: Char -> IO ()

-- retorna um valor puro envolvido de uma ação IO
return :: a -> IO a

Em vez de capturar apenas um caracter, podemos capturar uma linha inteira de informação. Podemos escrever getLine da seguinte maneira:

getLine :: IO String
getLine = do x <- getChar
	     if x == '\n' then
		return []
	     else
		do xs <- getLine
		   return (x:xs)

A função return não se comporta como em outras linguagens!
Lembre-se: return apenas pega um valor puro e o coloca no em um contexto. Ele não interrompe a execução.

3.15 Exercício 2

Escreva as instruções do else como Applicative

getLine :: IO String
getLine = do x <- getChar
	     if x == '\n' then
		return []
	     else
		do xs <- getLine
		   return (x:xs)

3.16 Exercício 2 - Resposta

getLine :: IO String
getLine = do x <- getChar
	     if x == '\n' then
		return []
	     else
		pure (x:) <*> getLine

A função inversa escreve uma String na saída padrão:

putStr :: String -> IO ()
putStr []     = return ()
putStr (x:xs) = do putChar x
		   putStr  xs

putStrLn :: String -> IO ()
putStrLn xs = do putStr xs
		 putChar 'n'

3.17 Exercício 3

Escreva a função putStrLn usando Applicative.

putStrLn :: String -> IO ()
putStrLn xs = do putStr xs
		 putChar '\n'

3.18 Exercício 3 - Resposta

putStrLn :: String -> IO ()
putStrLn xs = do sequenceA [putStr' xs, putChar 'n']
		 return ()

4 Funções de alta ordem para Monads

  • As funções de alta ordem possuem versões para Monads na biblioteca Control.Monad:
mapM :: Monad m => (a -> m b) -> [a] -> m [b]
mapM f []     = return []
mapM f (x:xs) = do y  <- f x
		   ys <- mapM f xs
		   return (y:ys)
  • Digamos que tenho a seguinte função:
conv :: Char -> Maybe Int
conv c | isDigit c = Just (digitToInt c)
       | otherwise = Nothing
  • Podemos aplicar mapM para obter:
> mapM conv "1234"
Just [1,2,3,4]
> mapM conv "12a4"
Nothing
  • Também temos a versão monádica de filter:
filterM :: Monad m => (a -> m Bool) -> [a] -> m [a]
filterM p []     = return []
filterM p (x:xs) = do b  <- p x
		      ys <- filter M p xs
		      return (if b then x:ys else ys)
  • Podemos gerar o conjunto das partes com essa função e o Monad List:
> filterM (\x -> [True, False]) [1,2,3]
[[1,2,3],[1,2],[1,3],[1],[2,3],[2],[3],[]]

🤨 🤨 🤨

  • Lembrando que o Monad listas representa uma computação não deterministica.

  • filterM: “para um certo elemento da lista, quais as possibilidades de selecioná-lo?”

  • \_ -> [False, True] diz que cada elemento pode existir ou não na lista!

  • Para cada elemento da lista, ele cria duas ramificações: uma em que aquele elemento existe e outra que ele não existe.
      []
    /    \
   [1]     []
  /  \    /   \
[1,2] [1] [2] []
...
  • filter seleciona elementos de uma lista
  • filterM seleciona possíveis eventos de uma sequência de computações
  • Considere esse outro exemplo:
f x | even x = [False]
    | otherwise = [True, False]

Qual a saída para filterM f [1, 2, 3]?

filterM f [1, 2, 3]

Saída:


[[1,3],[1],[3],[]]
  • Nesse caso geramos a combinação dos elementos ímpares.

  • E se nossa função for:

    g x | x == 0 = Nothing
    | even x = Just True
    | otherwise = Just False

    Qual a saída para filterM g [1, 2, 3, 0, 4] e filterM g [1, 2, 3, 4]?

filterM g [1, 2, 3, 0, 4]

Saída:


Nothing
filterM g [1, 2, 3, 4]

Saída:


Just [2,4]
  • o Nothing indica que a lista é inválida e não deve ser processada.
  • E com essa função?
h :: Int -> Writer String Bool
h x | x == 0 = writer (True, "Invalid! ")
    | even x = writer (True, "Valid! ")
    | otherwise = writer (False, "Discarded!" )

Qual a saída para filterM h [1, 2, 3, 0, 4] e filterM h [1, 2, 3, 4]?

filterM h [1, 2, 3, 0, 4]

Saída:


WriterT (Identity ([2,0,4],"Discarded!Valid! Discarded!Invalid! Valid! "))
filterM h [1, 2, 3, 4]

Saída:


WriterT (Identity ([2,4],"Discarded!Valid! Discarded!Valid! "))

4.1 Monads

4.2 Para saber mais - I

5 Disclaimer

Estes slides foram preparados para os cursos de Paradigmas de Programação e Desenvolvimento Orientado a Tipos na UFABC.

Este material pode ser usado livremente desde que sejam mantidos, além deste aviso, os créditos aos autores e instituições.