Tipos Dependentes - Tipos que dependem de valores

1 “Tipos Dependentes”: é de comer?

Em um post anterior falamos dos níveis onde vivem os termos, tipos, kinds… Claramente podemos fazer um valor depender de outro valor! Por exemplo, a função (+) recebe dois valores numéricos e devolve um novo valor que representa a soma dos valores recebidos. Que outras dependências será que conseguimos criar?

1.1 Dependência Tipo 1: Valor \(\to\) Valor

(a.k.a. funções no nível dos termos)

Em praticamente todas as linguagens de programação é possível fazer com que valores dependam de outros valores. Por exemplo, a função soma é capaz de dado um par de valores, devolver outro valor que depende exclusivamente do par escolhido como entrada:

soma :: Int -> Int -> Int
soma x y = x + y

A função ePar, devolve um valor booleano que depende do valor de entrada, inteiro, fornecido:

ePar :: Int -> Bool
ePar x = x `div` 2 == 0

1.2 Dependência tipo 2: Tipo \(\to\) Valor

(a.k.a. polimorfismo ad hoc)

Neste segundo tipo de dependência nós somos capazes de, a partir de um tipo, devolver valores diferentes. Ou seja, o valor passa a depender de um tipo. Em Haskell isso se manifesta como polimorfismo ad hoc e um exemplo de seu uso pode ser visto no próprio código de conversão de medidas onde a depender da unidade, recebemos uma sigla diferente. O código completo pode ser visto aqui, mas por conveniência reproduzimos a parte relevante abaixo:

data Grama
data Kilograma
data Onça
data Libra
data Pedra

class Unidade u where
  sigla :: String
  fator :: Floating a => a

instance Unidade Grama where
  sigla = "g"
  fator = 1

instance Unidade Kilograma where
  sigla = "kg"
  fator = 1000

instance Unidade Onça where
  sigla = "oz"
  fator = 28.35

instance Unidade Libra where
  sigla = "lb"
  fator = 453.59

instance Unidade Pedra where
  sigla = "st"
  fator = 14 * fator @Libra

No GHCI podemos fazer

> sigla @Grama
"g"

1.3 Dependência tipo 3: Tipo \(\to\) Tipo

(a.k.a. Funções no nível dos tipos, type families)

Neste terceiro tipo de dependência, aparecem finalmente os tipos que dependem de outros tipos. Esse é justamente o papel das Type Families que vimos no no post anterior.

Com type families podemos escrever códigos que quando recebem um tipo específico nos retornam um outro tipo. Por exemplo, poderiamos definir uma type family que quando recebe um tipo numérico devolve um outro tipo da mesma natureza (inteira, fracionária, complexa, …) com maior precisão (caso disponível). Neste contexto, quando esta type family receber um Int (que tem “apenas” 64 bits de precisão) poderiamos devolver Integer (com precisão arbitrária). Quando receber um Float (com 32 bits de precisão) poderíamos devolver Double (com 64 bits de precisão). O código abaixo mostra como tal type family poderia ser implementada:

type family MaisPreciso n where
  MaisPreciso Int     = Integer
  MaisPreciso Integer = Integer
  MaisPreciso Float   = Double
  MaisPreciso Double  = Double
  ...

Quando escrevemos a type family fica bem claro (apesar da sintaxe um tanto diferente) que ela é uma função que opera no nível dos tipos, da mesma maneira que funções comuns operam no nível dos termos.

1.4 Dependencia tipo 4: Valor \(\to\) Tipo

(a.k.a. Tipos dependentes )

Já vimos dependências Valor \(\to\) Valor, Tipo \(\to\) Valor, Tipo \(\to\) Tipo e agora vamos dar uma olhada no par final, Valor \(\to\) Tipo. Este último tipo de dependência é conhecico como Tipos Dependentes (já que o tipo depende do valor).

Linguagens que oferecem nativamente este tipo de dependência são raras, e entre elas estão Agda ou Idris por exemplo. Em linguagens como essas podemos fazer coisas semelhantes ao código abaixo (sintaxe fictícia):

newtype Valor m = MkValor Double deriving (Num)

converteValor::  (x :: String) -> (if x `contém` "R$" then Valor Real elseif x `contém` "US$" then Valor Dolar)
converteValor x = MkValor $ read (words x !! 2)

Vamos olhar com mais atenção o que está acontecendo nesta assinatura de função e como ela se diferencia dos casos anteriores de dependência que vimos. A função converteValor recebe uma String e devolve um termo do tipo Valor a. Valor é um tipo paramétrico (mais ainda, é um tipo fantasma) que guarda valores financeiros em Real ou Dolar. A diferença de converteValor quando comparada a outras funções que já vimos em posts anteriores é a de que o tipo de retorno não é fixo, nem determinado pelo local da chamada (como vimos quando falamos de higher-rank polymorphism). O tipo de retorno é determinado pelo conteúdo da string. Se ela contiver R$, então o tipo de retorno é Valor Real, se, por outro lado, ela contiver US$, o tipo de retorno é Valor Dolar. O tipo de retorno não é conhecido em tempo de compilação, nem no ponto da chamada!

Para que isso funcione no mundo real é preciso que o sistema de execução ( runtime system ) associado aos programas escritos nessas linguagens faça algumas coisas a mais, como o rastreamento e a verificação de tipos durante a execução (o que pode tornar a execução um pouco mais lenta). Durante a compilação todos os programas em Haskell passam por um processo chamado type erasure, onde todas as informações relativas aos tipos de cada um dos valores é apagado. Isto traz vantagens como economia de memória (já que não é preciso manter essa informação) e velocidade já que os tipos e eventuais especializações para tipos específicos para cada função utilizada podem ser resolvidos completamente, novamente, durante a compilação. Aliás, esta é uma característica de boa parte das linguagens compiladas estaticamente como C++, por exemplo.

Essas características fazem com que não haja uma maneira natural (tal qual em Idris ou em Agda) para utilizarmos tipos dependentes “de verdade” em Haskell. Por isso vamos fazer o que sempre fazemos em computação quando não temos as ferramentas certas para resolver um problema! Vamos dar uma roubadinha! ☺ (a.k.a. gambiarra, adaptação técnica, kludge).

Para alcançar tal façanha vamos usar de maneira bem criativa vários dos truques que vimos nos posts anteriores. Em especial, vamos empregar singleton types, tipos existenciais, e higher rank polymorphism.

2 Atravessando fronteiras

Em um post anterior nós falamos sobre promoção de tipos. Vamos rever o exemplo que demos na ocasião:

{-# LANGUAGE GADTs #-}
{-# LANGUAGE StandaloneKindSignatures #-}
{-# LANGUAGE DataKinds #-}

data PessoaTipo = Fisica | Juridica

type Pessoa :: PessoaTipo -> Type
data Pessoa t where
  Pessoa :: String -> Pessoa t

Com a extensão DataKinds ativada, este código cria as seguintes entidades de interesse:

• O tipo PessoaTipo, de kind Type, com dois construtores de valores Fisica e Juridica.
• Os tipos Fisica e Juridica (e seus construtores) de kind PessoaTipo.
• O tipo Pessoa, paramétrico que recebe como parâmetro um tipo de kind PessoaTipo com um construtor de valores Pessoa.

O tipo Pessoa é as vezes chamado de tipo de dados indexado (indexed data type). Em particular ele é indexado por um tipo do kind PessoaTipo.

As vantagens de escrever um tipo assim (como, por exemplo, para garantir já durante a compilação que uma função receba apenas valores Pessoa Fisica) já foram exploradas quando apresentamos tipos fantasmas.

Vamos supor que queremos criar uma função mkPessoa, semelhante à função converteValor que descrevemos acima, que recebe uma string que se começar com "F " é uma pessoa física e se começar com "J" é uma pessoa jurídica. Gostaríamos que ela tivesse uma cara parecida com o código abaixo:

mkPessoa :: String -> Pessoa t
mkPessoa nome = ...

Podemos enxergar o que queremos fazer com essa função como uma dependência do Tipo 4: sair de um valor no nível dos termos para um tipo (note, o tipo de retorno depende do valor da string). Ou seja, queremos atravessar uma das fronteiras (representadas pelas barras cinzas horizontais) na figura abaixo:

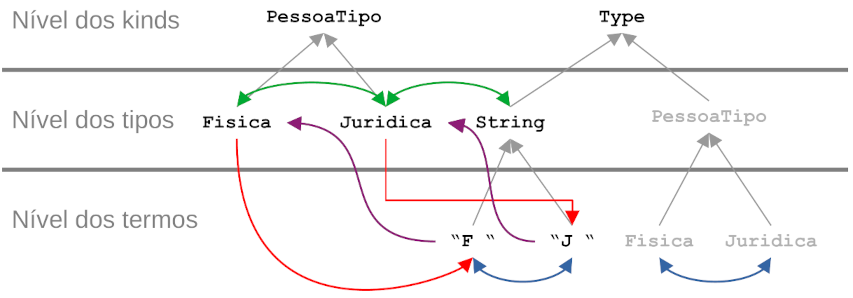
Nesta figura são mostradas algumas dependências dos tipos discutidos na seção anterior. As do Tipo 1 (valor \(\to\) valor) estão representadas em azul, as do Tipo 2 (tipo \(\to\) valor) estão em vermelho, as do Tipo 3 (tipo \(\to\) tipo) em verde e as do Tipo 4 (valor \(\to\) tipo) em roxo.

Atravessar a fronteira do nível dos tipos para o nível dos termos, é quase que trivial usando polimorfismo ad hoc. Já a travessia do nível dos termos para o nível dos tipos exige um pouco mais de trabalho.

O problema da função mkPessoa, tal qual descrita acima, é que não sabemos em tempo de compilação quem é t. Pode ser muito bem Fisica quanto Juridica. O chamador da função também não tem ideia, já que pode ter sido o usuário que digitou a string em um campo qualquer.

Já vimos como contornar esse problema antes! Aqui vamos aplicar tipos existenciais, e para isso vamos criar um tipo SomePessoa:

data SomePessoa where
  SomePessoa :: Pessoa t -> SomePessoa

E com isso, a assinatura da função mkPessoa passa a ser mkPessoa :: String -> SomePessoa. Perfeito. Mas ainda temos um probleminha, como criar a pessoa que vamos colocar dentro de SomePessoa?

3 Gambiarra 1: Usando Typeclasses

Vamos fazer uma primeira tentativa:

{-# LANGUAGE GADTs #-}
{-# LANGUAGE DataKinds #-}
{-# LANGUAGE StandaloneDeriving #-}
{-# LANGUAGE StandaloneKindSignatures #-}

module Main where

import Data.List
import Data.Kind

data PessoaTipo = Fisica | Juridica

type Pessoa :: PessoaTipo -> Type
data Pessoa t where
  Pessoa :: String -> Pessoa t
deriving instance Show (Pessoa t)

data SomePessoa where
  SomePessoa ::Pessoa t -> SomePessoa
deriving instance Show SomePessoa

mkPessoa :: String -> Maybe SomePessoa
mkPessoa s =
  case stripPrefix "F " s of
    Just n0 -> Just . SomePessoa $ Pessoa n0
    Nothing -> -- Ainda pode ser juridica
      SomePessoa . Pessoa <$> stripPrefix "J " s

Note que como estamos interessandos em segurança nos tipos, já aproveitamos e colocamos um Maybe no retorno. Sabe como são os usuários, vai que enviam uma string que não começa nem com "J " nem com "F ". Também adicionamos algumas instâncias de Show para podermos experimentar e ver os resultados facilmente no GHCI.

A função mkPessoa recebe uma string, verifica se começa com "F " e, neste caso devolve uma pessoa cujo nome é o que restou da string, sem o prefixo. O mesmo é feito para o caso de pessoa jurídica. Finalmente, caso nenhum dos prefixos seja reconhecido, devolve Nothing como era de se esperar.

O código compila e roda! Veja:

ghci> mkPessoa "F Leeloo Dallas"
Just (SomePessoa (Pessoa "Leeloo Dallas"))
ghci> mkPessoa "J Umbrella Corporation"
Just (SomePessoa (Pessoa "Umbrella Corporation"))
ghci> mkPessoa "X Multipass"
Nothing

Tudo certo então? Está resolvido? Não tão rápido! Esse código todo só funciona pois em momento nenhum usamos o fato de ser uma pessoa Fisica ou Juridica. Note a criação dos valores Pessoa, o tipo poderia ser Pessoa Fisica ou Pessoa Juridica em ambos que não faria diferença alguma! Como não usamos este fato o compilador quebra o galho e deixa passar.

Mas então, o que acontece se tentarmos usar o tipo da pessoa, para criar uma instância diferente de Show para cada caso, um para Fisica e outro para Juridica?

{-# LANGUAGE GADTs #-}
{-# LANGUAGE DataKinds #-}
{-# LANGUAGE StandaloneDeriving #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE StandaloneKindSignatures #-}
{-# LANGUAGE FlexibleContexts #-}

module Main where

import Data.List
import Data.Kind

data PessoaTipo = Fisica | Juridica

type Pessoa :: PessoaTipo -> Type
data Pessoa t where
  Pessoa :: String -> Pessoa t

instance Show (Pessoa Fisica) where
   show (Pessoa n) = "Fisica: " ++ n
instance Show (Pessoa Juridica) where
   show (Pessoa n) = "Juridica: " ++ n

data SomePessoa where
  SomePessoa :: Show (Pessoa t) => Pessoa t -> SomePessoa
deriving instance Show SomePessoa

mkPessoa :: String -> Maybe SomePessoa
mkPessoa s =
  case stripPrefix "F " s of
    Just n0 -> Just . SomePessoa $ Pessoa n0
    Nothing -> -- Ainda pode ser juridica
      SomePessoa . Pessoa <$> stripPrefix "J " s

Criamos uma instância de Show para Pessoa Fisica, outra para Pessoa Juridica e tivemos que colocar uma restrição adicional no nosso GADT existencial Show (Pessoa t). Essa última restrição é necessária já que agora não vale para qualquer t, mas apenas para aqueles que existe uma instância. De fato temos instâncias para todos os tipos de PessoaTipo, mas o compilador não é esperto o suficiente pra determinar isso sozinho. E, para tudo funcionar ainda adicionamos 2 extensões: FlexibleInstances e FlexibleContexts.

Quando tentamos compilar o código tomamos o seguinte erro:

	• Ambiguous type variable ‘t0’ arising from a use of ‘SomePessoa’
      prevents the constraint ‘(Show (Pessoa t0))’ from being solved.
      Probable fix: use a type annotation to specify what ‘t0’ should be.
      These potential instances exist:
	instance Show (Pessoa 'Juridica) -- Defined at src/Main.hs:22:10
	instance Show (Pessoa 'Fisica) -- Defined at src/Main.hs:20:10
    • In the second argument of ‘(.)’, namely ‘SomePessoa’
      In the first argument of ‘($)’, namely ‘Just . SomePessoa’
      In the expression: Just . SomePessoa $ Pessoa n0
   |
39 |     Just n0 -> Just . SomePessoa $ Pessoa n0
   |                       ^^^^^^^^^^

Eita! O que isso quer dizer? Basicamente o que já desconfiávamos acima, agora o compilador precisa saber qual tipo de pessoa se trata! E para isso ele sugere adicionarmos uma anotação de tipos! Vamos fazer isso usando uma aplicação de tipos e ver o que ocorre:

{-# LANGUAGE TypeApplications #-} -- Note a inclusão de uma nova extensão

mkPessoa :: String -> Maybe SomePessoa
mkPessoa s =
  case stripPrefix "F " s of
    Just n0 -> Just . SomePessoa @Fisica $ Pessoa n0
    Nothing -> -- Ainda pode ser juridica
      SomePessoa @Juridica. Pessoa <$> stripPrefix "J " s

E isso agora compila e roda que é uma beleza!

ghci> mkPessoa "F Leeloo Dallas"
Just (SomePessoa Fisica: Leeloo Dallas)
ghci> mkPessoa "J Umbrella Corporation"
Just (SomePessoa Juridica: Umbrella Corporation)
ghci> mkPessoa "X Multipass"
Nothing

Oba!! Tudo funciona como esperado. Conseguimos atravessar a fronteira! O tipo da pessoa criada varia conforme um valor que só sabemos em tempo de execução! Sucesso! \o/

E talvez você não tenha percebido, mas também fizemos o caminho contrário a typeclass Show. Conseguimos sair de um tipo e ir para o valor correspondente em tempo de execução! Ainda não viu? Vamos elaborar essa idea um pouco mais com uma nova typeclass, e uma função que basicamente é a inversa da função mkPessoa.

Assim como criamos instâncias da classe Show, vamos criar a nossa própria classe e as instâncias relevantes:

type PessoaToString :: PessoaTipo -> Constraint
class PessoaToString a where
  pessoaToString :: Pessoa a -> String
instance PessoaToString Fisica where
  pessoaToString (Pessoa n) = "F " ++ n
instance PessoaToString Juridica where
  pessoaToString (Pessoa n) = "J " ++ n

Assim como no caso de Show, também precisamos carregar essa typeclass no nosso tipo existencial:

data SomePessoa where
  SomePessoa :: (Show (Pessoa t), PessoaToString t) => Pessoa t -> SomePessoa
deriving instance Show SomePessoa

O tipo existencial esquece/mascara/esconde o tipo do parâmetro do tipo que ele contém (o tipo da pessoa no nosso exemplo). Por outro lado, aqueles presentes em cada um dos seus campos e em eventuais constraints são preservados. Isso ocorre pois as constraints funcionam como um parâmetro implícito, um dicionário que contém as implementações para os métodos da classe em questão, ou seja, não são diferentes de um campo adicional no GADT.

E já que dissemos que conseguimos ir e voltar nessa fronteira, vamos também criar a função inversa de mkPessoa que vamos chamar de unMkPessoa:

unMkPessoa :: SomePessoa -> String
unMkPessoa (SomePessoa p) = pessoaToString p

Aqui está o código completo:

{-# LANGUAGE GADTs #-}
{-# LANGUAGE DataKinds #-}
{-# LANGUAGE StandaloneDeriving #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE StandaloneKindSignatures #-}
{-# LANGUAGE FlexibleContexts #-}
{-# LANGUAGE TypeApplications #-}
{-# LANGUAGE AllowAmbiguousTypes #-}
{-# LANGUAGE ScopedTypeVariables #-}

module Main where

import Data.List
import Data.Kind

data PessoaTipo = Fisica | Juridica

type Pessoa :: PessoaTipo -> Type
data Pessoa t where
  Pessoa :: String -> Pessoa t

instance Show (Pessoa Fisica) where
   show (Pessoa n) = "Fisica: " ++ n
instance Show (Pessoa Juridica) where
   show (Pessoa n) = "Juridica: " ++ n

type PessoaToString :: PessoaTipo -> Constraint
class PessoaToString a where
  pessoaToString :: Pessoa a -> String
instance PessoaToString Fisica where
  pessoaToString (Pessoa n) = "F " ++ n
instance PessoaToString Juridica where
  pessoaToString (Pessoa n) = "J " ++ n

data SomePessoa where
  SomePessoa :: (Show (Pessoa t), PessoaToString t) => Pessoa t -> SomePessoa
deriving instance Show SomePessoa

mkPessoa :: String -> Maybe SomePessoa
mkPessoa s =
  case stripPrefix "F " s of
    Just n0 -> Just . SomePessoa @Fisica $ Pessoa n0
    Nothing -> -- Ainda pode ser juridica
      SomePessoa @Juridica. Pessoa <$> stripPrefix "J " s


unMkPessoa :: SomePessoa -> String
unMkPessoa (SomePessoa p) = pessoaToString p

E isso funciona exatamente como esperaríamos:

ghci> unMkPessoa <$> mkPessoa "F Leeloo Dallas"
Just "F Leeloo Dallas"
ghci> unMkPessoa <$> mkPessoa "J Umbrella Corporation"
Just "J Umbrella Corporation"
ghci> unMkPessoa <$> mkPessoa "X Multipass"
Nothing

Essa maneira de fazer as coisas (com typeclasses), contudo, é pouco mecânica (ou seja, é preciso tratar cada caso individualmente) e não é muito fácil de ser automatizada. Como se isso não bastasse, há também a possibilidade de esquecermos de implementar uma instância ou outra, errar a implementação de algum código nas “fronteiras” e o compilador não vai nos avisar. Por isso a maneira consagrada de se fazer isto em Haskell (até que a linguagem ofereça suporte nativo e completo para tipos dependentes) é utilizando singletons.

4 Gambiarra 2: Usando Singletons

Podemos aproveitar as melhores ideias da Gambiarra 1 e aprimorar as ideias que usamos com typeclasses usando-as em conjunto com outro conceito que vimos em um post anterior: singleton types.

Relembrando rapidamente: singleton types permitem que criemos uma bijeção entre o conjunto de valores possíveis para um tipo e o conjunto de tipos de um kind. Sendo mais preciso ainda, singleton types permitem a criação de um isomorfismo entre o conjunto de valores possíveis para um tipo e o conjunto de tipos de um kind.

Em nosso post anterior criamos um singleton type para o tipo Nat:

data Nat = Z | S Nat

type SNat :: Nat -> *
data SNat n where
  SZ :: SNat Z
  SS :: SNat n -> SNat (S n)

O tipo SNat é um tipo paramétrico que recebe um tipo do kind Nat. A sintaxe GADT nos permite amarrar os valores de SNat aos tipos Nat de tal forma que haja a bijeção desejada.

O singleton para o tipo PessoaTipo fica:

data PessoaTipo = Fisica | Juridica deriving Show

type SPessoaTipo :: PessoaTipo -> Type
data SPessoaTipo t where
  SFisica   :: SPessoaTipo Fisica
  SJuridica :: SPessoaTipo Juridica
deriving instance Show (SPessoaTipo t)

Note a semelhança com o tipo SNat. A regra é, cada tipo do kind de interesse mapeamos diretamente para um construtor do GADT. Esse mapeamento de um tipo para um construtor pode não ser único, como no caso de SNat, mas isso não é um problema contanto que os valores criados tenham um tipo cujo mapeamento é único.

Como isso nos ajuda a atravessar as fronteiras? A mágica toda acontece no pattern match de cada um dos construtores do GADT que traz para o contexto o parâmetro de tipos que precisamos!

Esse pattern match é muito mais poderoso do que pode parecer a primeira vista! Note que podemos fazer o seguinte agora:

-- Repetimos aqui a definição do tipo Pessoa para conveninência do leitor
type Pessoa :: PessoaTipo -> Type
data Pessoa t where
   Pessoa :: String -> Pessoa t
deriving instance Show (Pessoa t)

pegaCPF :: Pessoa Fisica -> String
pegaCPF pf = ...

pegaCNPJ :: Pessoa Juridica -> String
pegaCNPJ pj = ...

pegaDocumentoErrado :: Pessoa t -> String
pegaDocumentoErrado p   = pegaCPF p

pegaDocumento :: SPessoaTipo t -> Pessoa t -> String
pegaDocumento SFisica   = pegaCPF
pegaDocumento SJuridica = pegaCNPJ

A função pegaCPF só está definida para Pessoa Fisica. Então é preciso que o compilador consiga provar (durante a compilação, obviamente) que a pessoa em questão é física para permitir a chamada. Algo equivalente ocorre com a função pegaCNPJ. Se tentarmos compilar a função pegaDocumentoErrado receberemos um erro Couldn't match type 't' with 'Fisica' , que é o compilador nos dizendo que não conseguiu provar que p será sempre uma pessoa física. Este mesmo problema não está presente na função pegaDocumento. Nesta função o pattern match no singleton SPessoaTipo traz para o contexto a informação de quem é o tipo t (que é definido unicamente pela maneira que o GADT foi escrito), assim o compilador consegue provar que no branch de SFisica, t ~ Fisica e no branch SJuridica, t ~ Juridica e portanto permite as chamadas à pegaCPF e pegaCNPJ.

De fato, se vc tentar implementar a função incorretamente, como abaixo, você receberá um erro de compilação dizendo Couldn't match type 'Fisica' with 'Juridica e Couldn't match type 'Juridica' with 'Fisica.

pegaDocumento :: SPessoaTipo t -> Pessoa t -> String
pegaDocumento SFisica   = pegaCNPJ
pegaDocumento SJuridica = pegaCPF

Este tipo de casamento de padrões é chamado de casamento de padrões dependente (dependent pattern match).

Agora estamos prontos para sair de um representante de um tipo, um singleton, e ir para um valor utilizável em tempo de execução:

-- de um singleton, para um valor: Reflection
fromSing :: SPessoaTipo t -> PessoaTipo
fromSing SFisica = Fisica
fromSing SJuridica = Juridica

Este processo de travessia de fronteira (do nível dos tipos para o nível dos termos) é chamado de reflexão (reflection).

Podemos inclusive implementar funções para saber se uma pessoa é física ou jurídica!

pegaTipo :: SPessoaTipo t -> Pessoa t -> PessoaTipo
pegaTipo sgt _ = fromSing sgt

Mas pera aí! Isso ai é trapaça! Para “extrair” o tipo da Pessoa eu preciso passar um singleton a mais. Isso é inconveniente para dizer o mínimo! Quero tudo automático! Hum… Se tivesse um jeito de passar valores implicitamente por aí… Pera! Existe! Podemos usar class constraints e usar o mecanismo de passagem de dicionários que vem de graça!

Vamos começar definindo uma typeclass:

-- de um tipo, para um singleton: Reification
class SingI t where
    sing :: SPessoaTipo t
instance SingI Fisica where
    sing = SFisica
instance SingI Juridica where
    sing = SJuridica

Note a semelhança dessa typeclass com a typeclass PessoaToString que definimos na seção anterior. Em ambos os casos criamos instâncias da typeclass para cada um dos tipos (Fisica, Juridica) do nosso kind de interesse (PessoaTipo). Mais ainda, devolvemos um valor (no nível dos termos) que é ligado ao tipo (no nível dos tipos)!

Também note o seguinte: não dá para implementar uma instância incorreta já que o tipo do construtor do GADT tem que corresponder com o tipo definido como retorno da função sing que é definiddo pelo parâmetro da instância.

Veja:

instance SingI Fisica where
  -- sing :: SPessoaTipo Fisica
  -- qualquer outro construtor que não SFisica daria
  -- erro de compilação pois como SPessoaTipo é um singleton
  -- não há, por definição, nenhum outro valor com o mesmo tipo
  sing = SFisica

Como usamos isso? Bom, não é muito diferente do que fazíamos quando estávamos usando só typeclasses:

-- Versão antiga
pegaTipo :: SPessoaTipo t -> Pessoa t -> PessoaTipo
pegaTipo sgt _ = fromSing sgt

-- Versão nova
pegaTipo2 :: SingI t => Pessoa t -> PessoaTipo
pegaTipo2 = pegaTipo sing

No GHCI (não dê, por enquanto, muita atenção à criação da pessoa, vamos falar sobre isso em seguida):

ghci> pf = Pessoa "Leeloo Dallas" :: Pessoa Fisica
ghci> pj = Pessoa "Umbrella Corporation" :: Pessoa Juridica

-- Método original
ghci> pegaTipo SFisica pf
Fisica
ghci> pegaTipo SJuridica pj
Juridica

-- Mas a inferência de tipos consegue achar a instância correta!
-- Não precisamos escolher na mão.
ghci> pegaTipo sing pf
Fisica
ghci> pegaTipo sing pj
Juridica


-- Mais ainda, agora podemos criar uma função que some com o
-- singleton de uma só vez
ghci> pegaTipo2 pf
Fisica
ghci> pegaTipo2 pj
Juridica
ghci>

Batendo na mesma tecla: note que para recebermos o que precisamos automaticamente e tudo ficar amarradinho adicionamos a class constraint SingI ao tipo t da Pessoa na função pegaTipo2. Em outras palavras, pegaTipo e pegaTipo2 são essencialmente a mesma coisa, uma recebendo o parâmetro explicitamente e a outra implicitamente, respectivamente.

Bom, e a função mkPessoa que iniciou toda essa discussão? Aqui está o código:

mkPessoa :: SPessoaTipo t -> String -> Pessoa t
mkPessoa _ = Pessoa

Mas pera lá, de novo essa história? De onde tirar o singleton para passar como parâmetro para a criação da pessoa? Simples! Como o singleton vive no nível dos termos e a string que vamos usar para criar a pessoa também, basta fazer um mapeamento de string para o singleton, ou seja, é uma simples função de conversão (ou se quisermos falar mais bonito, uma Dependência Tipo 1 😜).

Vamos, lá, precisamos fazer os seguintes passos:

1. Precisamos mapear o texto a ser usado de prefixo para cada tipo de pessoa.
2. Neste ponto do campeonato, já estamos cansados de saber que quando o tipo de retorno de uma função depende de um valor, o tipo de retorno tem que ser existencial. Como precisamos um singleton cujo tipo muda conforme o tipo da pessoa para passar para a função mkPessoa, precisamos não só de um tipo existencial para o nosso singleton como também de uma função que vamos chamar de toSing que dado um PessoaTipo devolve o tipo existencial contendo o SPessoaTipo correspondente.
3. Criar uma função que, quando receber uma string verifique o prefixo (definido no passo 1) e devolva o tipo da pessoa, em um tipo existencial correspondente.
4. Assim como o PessoaTipo precisa ser encapsulado em um tipo existencial, Pessoa que é um tipo indexado em PessoaTipo também vai precisar de um tipo existencial para chamar de seu!

O passo 1 é bem direto e fácil de fazer:

pessoaTipoStr :: PessoaTipo -> String
pessoaTipoStr Fisica = "F "
pessoaTipoStr Juridica = "J "

O passo 2 exige um pouco mais de código, mas também é trivial:

-- Tipo existencial para o singleton SPessoaTipo
data SomeSPessoaTipo where
  SomeSPessoaTipo :: SPessoaTipo t -> SomeSPessoaTipo

-- Dado um valor PessoaTipo devolve um tipo existencial com singleton
toSing :: PessoaTipo -> SomeSPessoaTipo
toSing Fisica = SomeSPessoaTipo SFisica
toSing Juridica = SomeSPessoaTipo SJuridica

Este processo de sair de um valor no nível dos termos para um valor que representa um tipo é chamado de reificação (reification). Um tipo reificado (reified type) é um valor que representa um tipo. Em outras palavras o nosso singleton.

Para o passo 3 implementamos a função toSPessoaTipo:

toSPessoaTipo :: String -> Maybe SomeSPessoaTipo
toSPessoaTipo s
  | prefixo == pessoaTipoStr Fisica   = Just (toSing Fisica)
  | prefixo == pessoaTipoStr Juridica = Just (toSing Juridica)
  | otherwise                         = Nothing
  where
    prefixo = take 2 s

Essa função merece uma melhor explicação. A função toSPessoaTipo recebe a string que contém o prefixo do tipo da pessoa seguido do seu nome. Como usuários são usuários, precisamos prever o caso de recebermos uma string mal formada, por isso o tipo de retorno é Maybe. Como falamos acima, é preciso devolver um tipo existencial pois o compilador não tem como saber o tipo de retorno em tempo de compilação, essa informação só vai ser determinada quando o código for executado. Se o prefixo é inválido é devolvido Nothing, se por outro lado for um prefixo válido, criamos um tipo existencial com a função toSing que escrevemos no passo 2 e devolvemos dentro de um Just.

Passo 4, agora criamos o tipo existencial para pessoa.

-- Tipo existencial para o tipo de dados Pessoa. Note o armazenamento
-- do singleton representando o seu tipo
data SomePessoa where
    SomePessoa :: SPessoaTipo t -> Pessoa t -> SomePessoa
deriving instance Show SomePessoa

Note que guardamos em SomePessoa o sigleton usado durante a criação. Ele será útil para determinarmos mais adiante o tipo da pessoa. Aproveitamos e criamos também algumas funções auxiliares que nos serão úteis mais adiante:

-- Sinonimo para o construtor de SomePessoa
fromPessoa :: SPessoaTipo t -> Pessoa t -> SomePessoa
fromPessoa = SomePessoa

-- Constroi um SomePessoa. A peculiaridade aqui é que ele recebe o
-- valor PessoaTipo, o valor normal do nível dos termos. Não o singleton.
mkSomePessoa :: PessoaTipo -> String -> SomePessoa
mkSomePessoa dt = case toSing dt of
  SomeSPessoaTipo t -> fromPessoa t . mkPessoa t

A primeira função é apenas um sinônimo para o construtor de valores de SomePessoa. Já a função mkSomePessoa faz a ponte entre um valor dt do tipo PessoaTipo e o seu singleton. Para isto, a primeira coisa que a função faz é converter dt em um singleton com a chamada toSing dt. Para trazer as informações sobre o tipo para o contexto, ela então faz um pattern match em cujo corpo a pessoa é criada passando o singleton (mkPessoa t) e em seguida envelopada no seu tipo existencial (fromPessoa).

E com isso estamos prontos para finalmente criar a pessoa:

mkPessoa2 :: String -> Maybe SomePessoa
mkPessoa2 s = do
  sPessoaTipo <- toSPessoaTipo s
  return $ case sPessoaTipo of
    SomeSPessoaTipo t -> mkSomePessoa (fromSing t) (drop 2 s)

Note que já adicionamos também o Maybe no retorno porque, bem… usuários…

A função começa usando a função que criamos no passo 3, criando um SomeSPessoaTipo. Como ele vem embalado num Maybe, aproveitamos da do-syntax para retirá-lo da mônada. Em seguida, novamente fazemos um pattern match no tipo existencial para trazer as informações do nosso singleton para o contexto e simplesmente chamamos a função mkSomePessoa passando como parâmetro um valor do tipo PessoaTipo (que obtemos pela chamada de fromSing no singleton) e a string sem o prefixo.

Essa é a função que faz o pulo do gato! Note que amarramos o tipo da Pessoa ao tipo do singleton recebido como parâmetro. Ou seja, o tipo da pessoa criada vai depender de um valor sabido apenas em tempo de execução (já que tipo do singleton também só é sabido neste momento!). Note também que aqui estamos armazenando explicitamente o singleton que guarda o tipo de interesse. Contraste com o método implícito de utilizar constraints, que descrevemos na seção anterior, que implicitamente fazem o mesmo trabalho.

E, para chover no molhado: a função desempacota o SomeSPessoaTipo, repassa para mkPessoa e empacota o resultado em um SomePessoa (através da função mkSomePessoa). Essa parte é muito importante! Se você tentar fazer uma função que não reempacota o valor em um tipo existencial você vai receber erros do compilador! Lembre-se, uma vez dentro de um tipo existencial você não sai mais!

E finalmente, só para verificar que não estamos loucos fazendo um monte de código que é impossível de rodar, podemos também escrever a função inversa unMkSomePessoa:

unMkSomePessoa :: SomePessoa -> String
unMkSomePessoa (SomePessoa t (Pessoa n)) = pessoaTipoStr (fromSing t) ++ n

E tudo funciona!

ghci> unMkSomePessoa <$> mkPessoa2 "F Leeloo Dallas"
Just "F Leeloo Dallas"
ghci> unMkSomePessoa <$> mkPessoa2 "J Umbrella Corporation"
Just "J Umbrella Corporation"
ghci> unMkSomePessoa <$> mkPessoa2 "X Multipass"
Nothing

Aqui está o código completo para você ver tudinho de uma só vez!

{-# LANGUAGE GADTs #-}
{-# LANGUAGE DataKinds #-}
{-# LANGUAGE StandaloneDeriving #-}
{-# LANGUAGE StandaloneKindSignatures #-}

module Main where

import Data.Kind

-- Representa os tipos de pessoa: física ou juridica
data PessoaTipo = Fisica | Juridica deriving Show

-- O Singleton para PessoaTipo
type SPessoaTipo :: PessoaTipo -> Type
data SPessoaTipo t where
  SFisica   :: SPessoaTipo Fisica
  SJuridica :: SPessoaTipo Juridica
deriving instance Show (SPessoaTipo t)

-- Tipo existencial para o singleton SPessoaTipo
data SomeSPessoaTipo where
  SomeSPessoaTipo :: SPessoaTipo t -> SomeSPessoaTipo

-- de um singleton, para um valor: Reflection
fromSing :: SPessoaTipo t -> PessoaTipo
fromSing SFisica = Fisica
fromSing SJuridica = Juridica

-- Dado um valor PessoaTipo devolve um tipo existencial com singleton
toSing :: PessoaTipo -> SomeSPessoaTipo
toSing Fisica = SomeSPessoaTipo SFisica
toSing Juridica = SomeSPessoaTipo SJuridica

-- de um tipo, para um singleton: Reification
class SingI t where
    sing :: SPessoaTipo t
instance SingI Fisica where
    sing = SFisica
instance SingI Juridica where
    sing = SJuridica

pessoaTipoStr :: PessoaTipo -> String
pessoaTipoStr Fisica = "F "
pessoaTipoStr Juridica = "J "

toSPessoaTipo :: String -> Maybe SomeSPessoaTipo
toSPessoaTipo s
  | prefixo == pessoaTipoStr Fisica   = Just (toSing Fisica)
  | prefixo == pessoaTipoStr Juridica = Just (toSing Juridica)
  | otherwise                         = Nothing
  where
    prefixo = take 2 s

-- Tipo de dados indexado para representar uma pessoa física ou
-- jurídica. O tipo Pessoa é indexado por tipos do kind PessoaTipo.
type Pessoa :: PessoaTipo -> Type
data Pessoa t where
   Pessoa :: String -> Pessoa t
deriving instance Show (Pessoa t)

-- Versão antiga
pegaTipo :: SPessoaTipo t -> Pessoa t -> PessoaTipo
pegaTipo sgt _ = fromSing sgt

-- Versão nova
pegaTipo2 :: SingI t => Pessoa t -> PessoaTipo
pegaTipo2 = pegaTipo sing

-- Tipo existencial para o tipo de dados Pessoa. Note o armazenamento
-- do singleton representando o seu tipo
data SomePessoa where
    SomePessoa :: SPessoaTipo t -> Pessoa t -> SomePessoa
deriving instance Show SomePessoa

fromPessoa :: SPessoaTipo t -> Pessoa t -> SomePessoa
fromPessoa = SomePessoa

mkPessoa :: SPessoaTipo t -> String -> Pessoa t
mkPessoa _ = Pessoa

mkSomePessoa :: PessoaTipo -> String -> SomePessoa
mkSomePessoa dt = case toSing dt of
  SomeSPessoaTipo t -> fromPessoa t . mkPessoa t

mkPessoa2 :: String -> Maybe SomePessoa
mkPessoa2 s = do
  sPessoaTipo <- toSPessoaTipo s
  return $ case sPessoaTipo of
    SomeSPessoaTipo t -> mkSomePessoa (fromSing t) (drop 2 s)

unMkSomePessoa :: SomePessoa -> String
unMkSomePessoa (SomePessoa t (Pessoa n)) = pessoaTipoStr (fromSing t) ++ n

Você já deve ter reparado que nosso código está grande, e cheio de boilerplate code. Lembre-se! Começamos dizendo que Haskell ainda não tem suporte completo para tipos dependentes e que faríamos algumas adaptações criativas! Do jeito que as coisas estão fica até parecendo Java… 😔

De qualquer forma, ainda há alguns pontos que podem ser simplificados. Por exemplo, é muito comum criarmos uma função eliminadora (eliminator) quando lidamos com tipos existenciais. Por convenção, este tipo de função usa o prefixo with. O código para a funcã́o eliminadora segue sempre a mesma receita e usa o estilo de passagem de continuações (continuation passing style) ou CPS para os íntimos.

Vamos ver como isso ficaria no tipo existencial SomeSPessoaTipo:

withSome :: SomeSPessoaTipo -> (forall t. SPessoaTipo t -> v) -> v
withSome (SomeSPessoaTipo t) f = f t

E a sua aplicação:

-- Original
mkSomePessoa :: PessoaTipo -> String -> SomePessoa
mkSomePessoa dt = case toSing dt of
  SomeSPessoaTipo t -> fromPessoa t . mkPessoa t

-- Novo
mkSomePessoa' :: PessoaTipo -> String -> SomePessoa
mkSomePessoa' dt = withSome (toSing dt) $ \ t ->
  fromPessoa t . mkPessoa t

-- Original
mkPessoa2 :: String -> Maybe SomePessoa
mkPessoa2 s = do
  sPessoaTipo <- toSPessoaTipo s
  return $ case sPessoaTipo of
    SomeSPessoaTipo t -> mkSomePessoa (fromSing t) (drop 2 s)

-- Novo
mkPessoa2' :: String -> Maybe SomePessoa
mkPessoa2' s = do
  sPessoaTipo <- toSPessoaTipo s
  return $ withSome sPessoaTipo $ \t ->
    mkSomePessoa (fromSing t) (drop 2 s)

5 Automatizando e varrendo a gambiarra para debaixo do tapete: A biblioteca Singletons

A biblioteca singletons automatiza muitos dos passos que fizemos manualmente acima. Além de criar automaticamente boa parte do boilerplate que fizemos na mão, ela generaliza diversos conceitos que em nosso exemplo foram criados de forma extremamente específica para o nosso problema.

Entre outras coisas ela é capaz de gerar automaticamente muitas coisas que não geramos na mão. Por exemplo, ela é capaz de promover não apenas tipos para kinds, mas também funções para type families. Ou seja, ela gera automaticamente type families a partir de funções comuns! Ela inclusive é capaz de gerar o que seria o equivalente a aplicações parciais de type families, algo que hoje não é possível de fazer sem muita ginástica se formos usar apenas o que o GHC oferece de fábrica.

Mas e nosso exemplo, como que fica nessa biblioteca? Que mágica ela vai fazer?

Bom, a mágina é fortemente baseada em Template Haskell. Template Haskell é uma funcionalidade do GHC que nos permite fazer meta-programação durante a compilação do nosso código. Com isso, ela é capaz de gerar o boilerplate para nós. Para explicar, nada melhor que pormos a mão na massa:

{-# LANGUAGE EmptyCase                #-}
{-# LANGUAGE GADTs                    #-}
{-# LANGUAGE InstanceSigs             #-}
{-# LANGUAGE LambdaCase               #-}
{-# LANGUAGE ScopedTypeVariables      #-}
{-# LANGUAGE StandaloneDeriving       #-}
{-# LANGUAGE TemplateHaskell          #-}
{-# LANGUAGE TypeApplications         #-}
{-# LANGUAGE TypeFamilies             #-}
{-# LANGUAGE UndecidableInstances     #-}
{-# LANGUAGE StandaloneKindSignatures #-}
{-# LANGUAGE RankNTypes               #-}

import           Data.Kind
import           Data.Singletons
import           Data.Singletons.TH
import           Prelude.Singletons

$(singletons [d|
  data PessoaTipo = Fisica | Juridica deriving Show
  |])

Neste trecho de código envolvido por $(singletons [d| e |]) definimos o tipo de dado PessoaTipo. Também definimos o kind PessoaTipo, com 2 tipos. Até aqui, nenhuma novidade. A novidade é que automaticamente a biblioteca singleton também gerou para nós (entre outros):

• Um singleton SPessoaTipo (sinônimo de Sing PessoaTipo, Sing é uma data family), equivalente ao nosso SPessoaTipo
• Todas as instâncias necessárias de Fisica e Juridica para a classe SingI que é, essencialmente, a mesma que desenvolvemos (com a diferença que não serve apenas para PessoaTipo)
• As funções toSing e fromSing
• O tipo existencial para o singleton de PessoaTipo (SomeSing PessoaTipo)
• Funções eliminadoras de vários sabores
• …

Vamos dar uma olhada como fica o nosso código. Vamos tomar, primeiramente, como exemplo a função toSPessoaTipo. Mostramos abaixo a versão da função que usa o boilerplate feito a mão e a versão feita usando o boilerplate gerado automaticamente:

-- Usando o tipo existencial e o toSing que escrevemos na mão
toSPessoaTipo :: String -> Maybe SomeSPessoaTipo
toSPessoaTipo s
  | prefixo == pessoaTipoStr Fisica   = Just (toSing Fisica)
  | prefixo == pessoaTipoStr Juridica = Just (toSing Juridica)
  | otherwise                         = Nothing
  where
    prefixo = take 2 s

-- Usando o tipo existencial e toSing gerado pela biblioteca
toSPessoaTipo :: String -> Maybe (SomeSing PessoaTipo)
toSPessoaTipo s
  | prefixo == pessoaTipoStr Fisica   = Just (toSing Fisica)
  | prefixo == pessoaTipoStr Juridica = Just (toSing Juridica)
  | otherwise                         = Nothing
  where
    prefixo = take 2 s

Note que a implementação é idêntica, a menos da assinatura já que o nome do tipo existencial gerado pela biblioteca é ligeiramente diferente. Colocamos abaixo o código completo. Note como o tamanho dele é reduzido já que todo o boilerplate que tínhamos escrito antes já não é necessário.

{-# LANGUAGE DataKinds                #-}
{-# LANGUAGE EmptyCase                #-}
{-# LANGUAGE GADTs                    #-}
{-# LANGUAGE InstanceSigs             #-}
{-# LANGUAGE LambdaCase               #-}
{-# LANGUAGE ScopedTypeVariables      #-}
{-# LANGUAGE StandaloneDeriving       #-}
{-# LANGUAGE TemplateHaskell          #-}
{-# LANGUAGE TypeApplications         #-}
{-# LANGUAGE TypeFamilies             #-}
{-# LANGUAGE UndecidableInstances     #-}
{-# LANGUAGE StandaloneKindSignatures #-}
{-# LANGUAGE RankNTypes               #-}

module Main where

import           Data.Kind
import           Data.Singletons
import           Data.Singletons.TH
import           Prelude.Singletons

$(singletons [d|
  data PessoaTipo = Fisica | Juridica deriving Show
  |])

pessoaTipoStr :: PessoaTipo -> String
pessoaTipoStr Fisica = "F "
pessoaTipoStr Juridica = "J "

toSPessoaTipo :: String -> Maybe (SomeSing PessoaTipo)
toSPessoaTipo s
  | prefixo == pessoaTipoStr Fisica   = Just (toSing Fisica)
  | prefixo == pessoaTipoStr Juridica = Just (toSing Juridica)
  | otherwise                         = Nothing
  where
    prefixo = take 2 s

type Pessoa :: PessoaTipo -> Type
data Pessoa t where
   Pessoa :: String -> Pessoa t
deriving instance Show (Pessoa t)

pegaTipo :: SPessoaTipo t -> Pessoa t -> PessoaTipo
pegaTipo sgt _ = fromSing sgt

pegaTipo2 :: SingI t => Pessoa t -> PessoaTipo
pegaTipo2 = pegaTipo sing

data SomePessoa where
    SomePessoa :: Sing t -> Pessoa t -> SomePessoa
deriving instance Show SomePessoa

fromPessoa :: Sing t -> Pessoa t -> SomePessoa
fromPessoa = SomePessoa

mkPessoa :: Sing t -> String -> Pessoa t
mkPessoa _ = Pessoa

mkSomePessoa :: PessoaTipo -> String -> SomePessoa
mkSomePessoa dt = case toSing dt of
  SomeSing t -> fromPessoa t . mkPessoa t

mkPessoa2 :: String -> Maybe SomePessoa
mkPessoa2 s = do
  sPessoaTipo <- toSPessoaTipo s
  return $ case sPessoaTipo of
    SomeSing st -> mkSomePessoa (fromSing st) (drop 2 s)

unMkSomePessoa :: SomePessoa -> String
unMkSomePessoa (SomePessoa t (Pessoa n)) = pessoaTipoStr (fromSing t) ++ n

A biblioteca também gera funções eliminadoras:

-- Versão com pattern matching
mkSomePessoa :: PessoaTipo -> String -> SomePessoa
mkSomePessoa dt = case toSing dt of
  SomeSing t -> fromPessoa t . mkPessoa t

-- Versão com eliminadora
mkSomePessoa' :: PessoaTipo -> String -> SomePessoa
mkSomePessoa' dt = withSomeSing dt $ \ t ->
  fromPessoa t . mkPessoa t

Em resumo, se for trabalhar com sigletons, use a biblioteca e seja feliz!

6 Disclaimer

Estes slides foram preparados para os cursos de Paradigmas de Programação e Desenvolvimento Orientado a Tipos na UFABC.

Este material pode ser usado livremente desde que sejam mantidos, além deste aviso, os créditos aos autores e instituições.